Question

20．若x，y满足约束条件$\left\{\begin{array}{l}{x+y≥1}\\{-x+y≤1}\\{2x-y≤2}\end{array}\right.$．
（1）求目标函数z=$\frac{1}{2}x$-y+$\frac{1}{2}$的最值；
（2）若目标函数z=ax+2y仅在点（1，0）处取得最小值，求a的取值范围．
（3）求点P（x，y）到直线y=-x-2的距离的最大值；
（4）z=x²+y²-10y+25的最小值；
（5）z=$\frac{2y+1}{x+1}$的范围．

Answer 1

分析 （1）作出可行域，利用目标函数的几何意义即可得到结论；
（2）若目标函数z=ax+2y仅在点（1，0）处取得最小值，判断目标函数的斜率关系，即可得到结论；
（3）由可行域可得C到直线的距离最大，运用点到直线的距离公式可得；
（4）配方可得z表示点（x，y）到点（0，5）的距离的平方，由可行域可得A到（0，5）的距离最小；
（5）z=$\frac{2y+1}{x+1}$=2•$\frac{y-（-\frac{1}{2}）}{x-（-1）}$的几何意义是点（x，y）与点E（-1，-$\frac{1}{2}$）的斜率的2倍．由可行域可得AE的斜率最小，BE的斜率最大．

解答 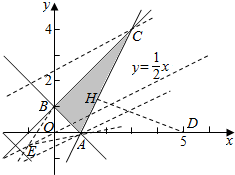解：（1）画出不等式组表示的可行域，如图：
求得A（1，0），B（0，1），C（3，4），
作出直线l₀：y=$\frac{1}{2}$x，平移直线l₀，
当直线经过点C时，z=$\frac{1}{2}x$-y+$\frac{1}{2}$取得最小值，且为-2；
当直线经过点A时，z=$\frac{1}{2}x$-y+$\frac{1}{2}$取得最大值，且为1．
（2）目标函数z=ax+2y仅在点（1，0）处取得最小值，
若a=0，则目标函数为z=2y，此时y=$\frac{z}{2}$，满足条件．
若a≠0，则目标函数为y=-$\frac{a}{2}$x+$\frac{z}{2}$，
若a＞0，则斜率k=-$\frac{a}{2}$＜0，
要使目标函数z=ax+2y仅在点（1，0）处取得最小值，
则-$\frac{a}{2}$＞-1，即a＜2，此时0＜a＜2；
若a＜0，则斜率k=-$\frac{a}{2}$＞0，
要使目标函数z=ax+2y仅在点（1，0）处取得最小值，
则-$\frac{a}{2}$＜2，即a＞-4，此时-4＜a＜0，
综上-4＜a＜2，即a的取值范围（-4，2）；
（3）作出直线y=-x-2，显然点C（3，4）到直线的距离最大，
且为d=$\frac{|3+4+2|}{\sqrt{2}}$=$\frac{11\sqrt{2}}{2}$；
（4）z=x²+y²-10y+25=x²+（y-5）²，
即为点（x，y）到点（0，5）的距离的平方，
由可行域可得，显然A（1，0）到点（0，5）的距离最小，
且为$\sqrt{26}$，即有z的最小值为26；
（5）z=$\frac{2y+1}{x+1}$=2•$\frac{y-（-\frac{1}{2}）}{x-（-1）}$的几何意义是点（x，y）与点E（-1，-$\frac{1}{2}$）的斜率的2倍．
由可行域可得显然AE的斜率最小，BE的斜率最大．
由k_AE=$\frac{0+\frac{1}{2}}{1+1}$=$\frac{1}{4}$，k_BE=$\frac{1+\frac{1}{2}}{0+1}$=$\frac{3}{2}$，
可得z的最小值为$\frac{1}{2}$，最大值为3．

点评 本题主要考查线性规划的应用，根据目标函数的几何意义是解决本题的关键．注意使用数形结合．