
某种产品的广告费支出 (单位:万元)与销售额
(单位:万元)与销售额 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
广告费支出 | 2 | 4 | 5 | 6 | 8 |
销售额 | 30 | 40 | 60 | 50 | 70 |
 ,
,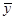 的值并求点
的值并求点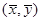 对应的复数
对应的复数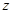 ;
;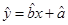 。
。 | 2 | 4 | 5 | 6 | 8 |
 | 30 | 40 | 60 | 50 | 70 |
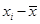 | | | | | |
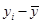 | | | | | |
 | | | | | |
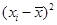 | | | | | |
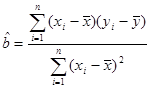 )
) (1)5,50, (2)
(2)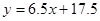
解析试题分析:(1)
科目:高中数学
来源:
题型:解答题
已知某池塘养殖着鲤鱼和鲫鱼,为了估计这两种鱼的数量,养殖者从池塘中捕出两种鱼各
科目:高中数学
来源:
题型:解答题
某班同学利用寒假在5个居民小区内选择两个小区逐户进行一次“低碳生活习惯”的调查,以计算每户每月的碳排放量.若月排放量符合低碳标准的称为“低碳族”,否则称为“非低碳族”.若小区内有至少
科目:高中数学
来源:
题型:解答题
为了解目前老年人居家养老还是在敬老院养老的意向,共调查了50名老年人,其中男性明确表示去敬老院养老的有5人,女性明确表示居家养老的有10人,已知在全部50人中随机地抽取1人明确表示居家养老的概率为
科目:高中数学
来源:
题型:解答题
假设关于某设备使用年限x(年)和所支出的维修费用y(万元)有如下统计资料:若由资料知,y对x呈线性相关关系,试求:
科目:高中数学
来源:
题型:解答题
某校从参加市联考的甲、乙两班数学成绩110分以上的同学中各随机抽取8人,将这16人的数学成绩编成如下茎叶图.
科目:高中数学
来源:
题型:解答题
某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本,得频率分布表如下:
科目:高中数学
来源:
题型:解答题
在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2, ,6)的同学所得成绩,且前5位同学的成绩如下:
科目:高中数学
来源:
题型:解答题
(本小题满分12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
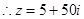
(2)
2 4 5 6 8 
30 40 60 50 70 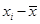
-3 -1 0 1 3 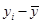
-20 -10 10 0 20 
60 10 0 0 60 

单元测试四川教育出版社系列答案
少年素质教育报综合检测系列答案
清华绿卡期末卷系列答案
课后练习专题精析系列答案
双测AB卷系列答案
新思维成才典对典系列答案
各地初中期末汇编系列答案
单元双测全优测评卷系列答案
师大测评卷期末点津系列答案
课堂同步提优系列答案
 只,给每只鱼做上不影响其存活的标记,然后放回池塘,待完全混合后,再每次从池塘中随机的捕出
只,给每只鱼做上不影响其存活的标记,然后放回池塘,待完全混合后,再每次从池塘中随机的捕出 只鱼,记录下其中有记号的鱼的数目,立即放回池塘中。这样的记录做了
只鱼,记录下其中有记号的鱼的数目,立即放回池塘中。这样的记录做了 次,并将记录获取的数据做成以下的茎叶图。
次,并将记录获取的数据做成以下的茎叶图。
(Ⅰ)根据茎叶图计算有记号的鲤鱼和鲫鱼数目的平均数,并估计池塘中的鲤鱼和鲫鱼的数量;
(Ⅱ)为了估计池塘中鱼的总重量,现从中按照(Ⅰ)的比例对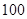 条鱼进行称重,据称重鱼的重量介于
条鱼进行称重,据称重鱼的重量介于 (单位:千克)之间,将测量结果按如下方式分成九组:第一组
(单位:千克)之间,将测量结果按如下方式分成九组:第一组 、第二组
、第二组 ;……,第九组
;……,第九组 。右图是按上述分组方法得到的频率分布直方图的一部分。
。右图是按上述分组方法得到的频率分布直方图的一部分。
①估计池塘中鱼的重量在 千克以上(含
千克以上(含 千克)的条数;
千克)的条数;
②若第二组、第三组、第四组鱼的条数依次成公差为 的等差数列,请将频率分布直方图补充完整;
的等差数列,请将频率分布直方图补充完整;
③在②的条件下估计池塘中鱼的重量的众数、中位数及估计池塘中鱼的总重量;
(Ⅲ)假设随机地从池塘逐只有放回的捕出 只鱼中出现鲤鱼的次数为
只鱼中出现鲤鱼的次数为 ,求
,求 的数学期望。
的数学期望。 的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区”.已知备选的5个居民小区中有三个非低碳小区,两个低碳小区.
的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区”.已知备选的5个居民小区中有三个非低碳小区,两个低碳小区.
(1)求所选的两个小区恰有一个为“非低碳小区”的概率;
(2)假定选择的“非低碳小区”为小区 ,调查显示其“低碳族”的比例为
,调查显示其“低碳族”的比例为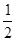 ,数据如图1所示,经过同学们的大力宣传,三个月后,又进行了一次调查,数据如图2所示,问这时小区
,数据如图1所示,经过同学们的大力宣传,三个月后,又进行了一次调查,数据如图2所示,问这时小区 是否达到“低碳小区”的标准?
是否达到“低碳小区”的标准?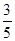 。
。
(1)请根据上述数据建立一个2×2列联表;(2)居家养老是否与性别有关?请说明理由。
参考数据: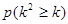
0.100 0.050 0.025 0.010 0.001 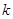
2.706 3.841 5.024 6.635 10.828
(1)回归直线方程;(2)估计使用年限为10年时,维修费用约是多少?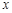
2 3 4 5 6 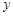
2.2 3.8 5.5 6.5 7.0 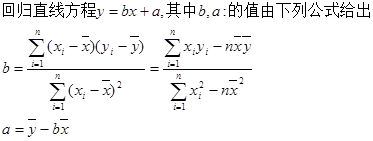 .
.
(Ⅰ)茎叶图中有一个数据污损不清(用△表示),若甲班抽出来的同学平均成绩为122分,试推算这个污损的数据是多少?
(Ⅱ)现要从成绩在130分以上的5位同学中选2位作数学学习方法介绍,请将所有可能的结果列举出来,并求选出的两位同学不在同一个班的概率.
(1)写出表中①②位置的数据;组号 分组 频数 频率 第一组 [230,235) 8 0.16 第二组 [235,240) ① 0.24 第三组 [240,245) 15 ② 第四组 [245,250) 10 0.20 第五组 [250,255] 5 0.10 合 计 50 1.00
(2)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,分别求第三、四、五各组参加考核人数;
(3)在(2)的前提下,高校决定在这6名学生中录取2名学生,求2人中至少有1名是第四组的概率.
(1)求第6位同学的成绩x6,及这6位同学成绩的标准差s;编号n
1
2
3
4
5
成绩xn
70
76
72
70
72
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
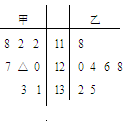
某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,可见部分如下(阴影部分为损坏数据),
据此解答如下问题:
(1) 求本次测试成绩的中位数,并求频率分布直方图中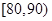 的矩形的高(用小数表示);
的矩形的高(用小数表示);
(2) 若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在[90,100]之间的概率.
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号