
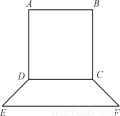
要制作一个如图的框架(单位:m),要求所围成的总面积为19.5(m2),其中ABCD是一个矩形,EFCD是一个等腰梯形,梯形高h= AB,tan∠FED=
AB,tan∠FED= ,设AB=x m,BC=y m.
,设AB=x m,BC=y m.
(1) 求y关于x的表达式;
(2) 如何设计x,y的长度,才能使所用材料最少?
(1)y=
 x
x ,(2)AB=3 m,BC=4 m时,能使整个框架用材料最少.
,(2)AB=3 m,BC=4 m时,能使整个框架用材料最少.
【解析】
试题分析:(1)解实际问题应用题,关键在于正确理解题意,正确列出等量关系. 在等腰梯形CDEF中,高DH= AB=
AB= x,EH=
x,EH= =
= ×
× x=
x= x,∴
x,∴  =xy+
=xy+

 x=xy+
x=xy+ x2,∴ y=
x2,∴ y=
 x.求函数解析式不要忘记交代定义域,∵ x>0,y>0,∴
x.求函数解析式不要忘记交代定义域,∵ x>0,y>0,∴ 
 x>0,解之得0<x<
x>0,解之得0<x< .(2)所用材料就是计算周长,在Rt△DEH中,∵ tan∠FED=
.(2)所用材料就是计算周长,在Rt△DEH中,∵ tan∠FED= ,∴ sin∠FED=
,∴ sin∠FED= ,∴ DE=
,∴ DE= =
= x×
x× =
= x,∴ l=(2x+2y)+2×
x,∴ l=(2x+2y)+2× x+
x+ =2y+6x =
=2y+6x =
 x+6x=
x+6x= +
+ x,由基本不等式
x,由基本不等式 +
+ x≥2
x≥2 =26,当且仅当
=26,当且仅当 =
= x,即x2=9,即x=3时取等号,此时AB=3 m,BC=4 m时,能使整个框架用材料最少.
x,即x2=9,即x=3时取等号,此时AB=3 m,BC=4 m时,能使整个框架用材料最少.
【解析】
(1) 如图,在等腰梯形CDEF中,DH是高.
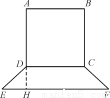
依题意:DH= AB=
AB= x,EH=
x,EH= =
= ×
× x=
x= x, (3分)
x, (3分)
∴  =xy+
=xy+

 x=xy+
x=xy+ x2,
x2,
∴ y=
 x. (5分)
x. (5分)
∵ x>0,y>0,
∴ 
 x>0,解之得0<x<
x>0,解之得0<x< .
.
∴ 所求表达式为y=
 x
x . 7分(没有定义域扣2分)
. 7分(没有定义域扣2分)
(2) 在Rt△DEH中,∵ tan∠FED= ,∴ sin∠FED=
,∴ sin∠FED= ,
,
∴ DE= =
= x×
x× =
= x, 9分
x, 9分
∴ l=(2x+2y)+2× x+
x+ =2y+6x 10分
=2y+6x 10分
=
 x+6x=
x+6x= +
+ x≥2
x≥2 =26, 13分
=26, 13分
当且仅当 =
= x,即x2=9,即x=3时取等号, 15分
x,即x2=9,即x=3时取等号, 15分
此时y=
 x=4,
x=4,
∴ AB=3 m,BC=4 m时,能使整个框架用材料最少. 16分
考点:基本不等式求最值


科目:高中数学 来源:2016届江苏省(集团)高一下学期期中考试数学试卷(解析版) 题型:填空题
已知等比数列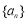 满足
满足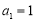 ,
,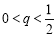 ,且对任意正整数
,且对任意正整数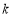 ,
,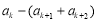 仍是该数列中的某一项,则公比
仍是该数列中的某一项,则公比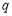 为____________.
为____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com