
如图所示,在直四棱柱ABCD-A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC.
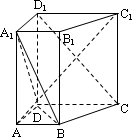
(Ⅰ)求证:D1C⊥AC1;
(Ⅱ)设E是DC上一点,试确定E的位置,使D1E∥平面A1BD,并说明理由.
|
解:(1)证明:在直四棱柱ABCD-A1B1C1D1中, 连结C1D, ∵DC=DD1, ∴四边形DCC1D1是正方形. ∴DC1⊥D1C. 又AD⊥DC,AD⊥DD1,DC∩DD1=D, ∴AD⊥平面DCC1D1, D1C ∴AD⊥D1C. ∵AD∩DC1=D ∴D1C⊥平面ADC1, 又AC1 ∴DC1⊥AC1 (2)连结AD1,连结AE, 设AD1∩A1D=M, BD∩AE=N,连结MN, ∵平面AD1E∩平面A1BD, 须使MN∥D1E, 又M是AD1的中点, ∴N是AE的中点. 又易知△ABN≌△EDN, ∴AB=DE. 即E是DC的中点. 综上所述,当E是DC的中点时,可使D1E∥平面A1BD. |


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
 19、如图所示,在直四棱柱ABCD-A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上一点.
19、如图所示,在直四棱柱ABCD-A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上一点.查看答案和解析>>
科目:高中数学 来源: 题型:
 18、如图所示,在直四棱柱ABCD-A1B1C1D1中,DB⊥AC,点M是棱BB1上一点.
18、如图所示,在直四棱柱ABCD-A1B1C1D1中,DB⊥AC,点M是棱BB1上一点.查看答案和解析>>
科目:高中数学 来源: 题型:
 16、如图所示,在直四棱柱M中,DB=BC,MN,点EN是棱MN上一点.
16、如图所示,在直四棱柱M中,DB=BC,MN,点EN是棱MN上一点.查看答案和解析>>
科目:高中数学 来源:同步题 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2011年高三数学第一轮复习巩固与练习:空间中的垂直关系(解析版) 题型:解答题
 如图所示,在直四棱柱ABCD-A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上一点.
如图所示,在直四棱柱ABCD-A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com