
【题目】设数列{an}的前n和为Sn , a1=1,Sn=nan﹣2n2+2n(n∈N*).
(1)求证:数列{an}为等差数列,并分别写出an和Sn关于n的表达式;
(2)是否存在自然数n,使得S1+ ![]() +
+ ![]() +…+
+…+ ![]() +2n=1124?若存在,求出n的值; 若不存在,请说明理由;
+2n=1124?若存在,求出n的值; 若不存在,请说明理由;
(3)设cn= ![]() (n∈N*),Tn=c1+c2+c3+…+cn(n∈N*),若不等式Tn>
(n∈N*),Tn=c1+c2+c3+…+cn(n∈N*),若不等式Tn> ![]() (m∈Z),对n∈N*恒成立,求m的最大值.
(m∈Z),对n∈N*恒成立,求m的最大值.
【答案】
(1)证明:由 ![]() ,得
,得 ![]() ,
,
相减得an=nan﹣(n﹣1)an﹣1﹣4n+4(n﹣1)an﹣(n﹣1)an﹣1=4(n﹣1)an﹣an﹣1=4(n≥2).
故数列{an}是首项为1,公差为4的等差数列.∴an=1+4(n﹣1)=4n﹣3.Sn= ![]() =2n2﹣n.
=2n2﹣n.
(2)解:由(1)可得: ![]() =2n﹣1.
=2n﹣1.
∴ ![]() ,
,
由n2+2n=1124,得n=10,即存在满足条件的自然数n=10
(3)解: ![]() =
= ![]() ,
,
∵ ![]() ,
,
∴Tn<Tn+1,即Tn单调递增,故 ![]() 要使
要使 ![]() 恒成立,只需
恒成立,只需 ![]() 成立,即m<8(m∈Z).
成立,即m<8(m∈Z).
故符合条件m的最大值为7
【解析】(1)由 ![]() ,利用递推关系an=
,利用递推关系an= ![]() 可得an﹣an﹣1=4(n≥2).利用等差数列的通项公式与求和公式即可得出:an , Sn . (2)由(1)可得:
可得an﹣an﹣1=4(n≥2).利用等差数列的通项公式与求和公式即可得出:an , Sn . (2)由(1)可得: ![]() =2n﹣1.利用等差数列的求和公式即可得出.(3)利用“裂项求和方法”、数列的单调性即可得出.
=2n﹣1.利用等差数列的求和公式即可得出.(3)利用“裂项求和方法”、数列的单调性即可得出.
【考点精析】掌握数列的前n项和和数列的通项公式是解答本题的根本,需要知道数列{an}的前n项和sn与通项an的关系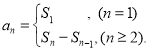 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
【题目】G为△ADE的重心,点P为△DEG内部(含边界)上任一点,B,C均为AD,AE上的三等分点(靠近点A), ![]() =α
=α ![]() +β
+β ![]() (α,β∈R),则α+
(α,β∈R),则α+ ![]() β的范围是( )
β的范围是( )
A.[1,2]
B.[1, ![]() ]
]
C.[ ![]() ,2]
,2]
D.[ ![]() ,3]
,3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 且函数y=f(x)﹣x恰有3个不同的零点,则实数a的取值范围是( )
且函数y=f(x)﹣x恰有3个不同的零点,则实数a的取值范围是( )
A.(0,+∞)
B.[﹣1,0)
C.[﹣1,+∞)
D.[﹣2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=2x﹣1.
(1)求f(3)+f(﹣1);
(2)求f(x)在R上的解析式;
(3)求不等式﹣7≤f(x)≤3的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=|x﹣2|+|x+1|+2|x+2|.
(1)求证:f(x)≥5;
(2)若对任意实数x,15﹣2f(x)<a2+ ![]() 都成立,求实数a的取值范围.
都成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3+ ![]() x2在x=﹣1处取得极大值,记g(x)=
x2在x=﹣1处取得极大值,记g(x)= ![]() .程序框图如图所示,若输出的结果S>
.程序框图如图所示,若输出的结果S> ![]() ,则判断框中可以填入的关于n的判断条件是( )
,则判断框中可以填入的关于n的判断条件是( ) 
A.n≤2014?
B.n≤2015?
C.n>2014?
D.n>2015?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于命题的说法错误的是( )
A.命题“若x2﹣3x+2=0,则x=1”的逆否命题为“若x≠1,则x2﹣3x+2≠0”
B.“a=2”是“函数f(x)=logax在区间(0,+∞)上为增函数”的充分不必要条件
C.若命题P:n∈N,2n>1000,则﹣P:n∈N,2n≤1000
D.命题“x∈(﹣∞,0),2x<3x”是真命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com