
如图所示,在面积为9的三角形ABC中,tanA=![]() ,且
,且![]() .
.
(1)建立适合的坐标系,求以AB,AC所在直线为渐近线且过点D的双曲线的方程;
(2)过D分别作AB,AC所在直线的垂线DE,DF(E,F为垂足),求![]() 的值.
的值.

科目:高中数学 来源: 题型:
 某城市计划在如图所示的空地ABCD上竖一块长方形液晶广告屏幕MNEF,宣传该城市未来十年计划、目标等相关政策.已知四边形ABCD是边长为30m的正方形,电源在点P处,点P到边AD、AB的距离分别为9m,3m,且MN~NE=16~9,线段MN必过点P,端点M、N分别在边AD、AB上,设AN=xm,液晶广告屏幕MNEF的面积为Sm2.
某城市计划在如图所示的空地ABCD上竖一块长方形液晶广告屏幕MNEF,宣传该城市未来十年计划、目标等相关政策.已知四边形ABCD是边长为30m的正方形,电源在点P处,点P到边AD、AB的距离分别为9m,3m,且MN~NE=16~9,线段MN必过点P,端点M、N分别在边AD、AB上,设AN=xm,液晶广告屏幕MNEF的面积为Sm2.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,已知二次函数y=-x2+9,矩形ABOC的顶点A在第一象限内,且A在抛物线上,顶点B、C分别在y轴、x轴上,设点A的坐标为(x,y).
如图所示,已知二次函数y=-x2+9,矩形ABOC的顶点A在第一象限内,且A在抛物线上,顶点B、C分别在y轴、x轴上,设点A的坐标为(x,y).查看答案和解析>>
科目:高中数学 来源: 题型:
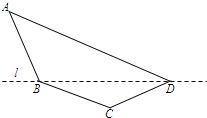 (2012•南京二模)某单位设计一个展览沙盘,现欲在沙盘平面内,布设一个对角线在l上的四边形电气线路,如图所示.为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,要求∠A和∠C互补,且AB=BC.
(2012•南京二模)某单位设计一个展览沙盘,现欲在沙盘平面内,布设一个对角线在l上的四边形电气线路,如图所示.为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,要求∠A和∠C互补,且AB=BC.查看答案和解析>>
科目:高中数学 来源: 题型:
 (理科)2013年将举办的第十二届中国•东海国际水晶节,主题为“水晶之都•福如东海”,于9月28日在国内唯一水晶博物馆正式开幕.为方便顾客,在休息区200m2的矩形区域内布置了如图所示的休闲区域(阴影部分),已知下方是两个相同的矩形.在休闲区域四周各留下1m宽的小路,若上面矩形部分与下方矩形部分高度之比为1:2.问如何设计休息区域,可使总休闲区域面积最大.
(理科)2013年将举办的第十二届中国•东海国际水晶节,主题为“水晶之都•福如东海”,于9月28日在国内唯一水晶博物馆正式开幕.为方便顾客,在休息区200m2的矩形区域内布置了如图所示的休闲区域(阴影部分),已知下方是两个相同的矩形.在休闲区域四周各留下1m宽的小路,若上面矩形部分与下方矩形部分高度之比为1:2.问如何设计休息区域,可使总休闲区域面积最大.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com