
在直角坐标系xOy中,直线l的参数方程为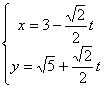 (t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=2
(t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=2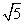 sin θ.
sin θ.
(1)求圆C的直角坐标方程;
(2)设圆C与直线l交于点A、B,若点P的坐标为(3,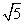 ),求|PA|+|PB|.
),求|PA|+|PB|.
解:(1)由ρ=2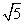 sin θ,得x2+y2-2
sin θ,得x2+y2-2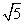 y=0,
y=0,
即x2+(y-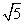 )2=5. -----------5分
)2=5. -----------5分
(2)法一:将l的参数方程代入圆C的直角坐标方程,
得(3-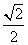 t)2+(
t)2+(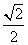 t)2=5,
t)2=5,
即t2-3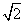 t+4=0.
t+4=0.
由于Δ=(3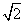 )2-4×4=2>0,故可设t1,t2是上述方程的两实根,
)2-4×4=2>0,故可设t1,t2是上述方程的两实根,
所以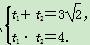
又直线l过点P(3,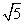 ),
),
故由上式及t的几何意义得|PA|+|PB|=|t1|+|t2|=t1+t2=3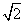 .-----------10分
.-----------10分
(2)法二:因为圆C的圆心为(0,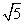 ),半径r=
),半径r=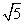 ,
,
直线l的普通方程为:y=-x+3+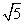 .
.
由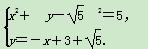 得x2-3x+2=0.
得x2-3x+2=0.
解得: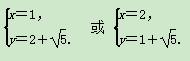
不妨设A(1,2+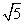 ),B(2,1+
),B(2,1+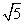 ),
),
又点P的坐标为(3,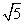 ),
),
故|PA|+|PB|=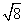 +
+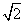 =3
=3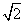 . -----------10分
. -----------10分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
设甲、乙、丙三个乒乓球协会的运动员人数分别为27,9,18,先采用分层抽样的方法从这三个协会中抽取6名运动员参加比赛。
(Ⅰ)求应从这三个协会中分别抽取的运动员人数;
(Ⅱ)将抽取的6名运动员进行编号,编号分别为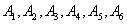 ,从这6名运动员中随机抽取2名参加双打比赛。
,从这6名运动员中随机抽取2名参加双打比赛。
(i)用所给编号列出所有可能的结果;
(ii)设A为事件“编号为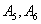 的两名运动员至少有一人被抽到”,求事件A发生的概率。
的两名运动员至少有一人被抽到”,求事件A发生的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
“孝敬父母。感恩社会”是中华民族的传统美德。从出生开始,父母就对我们关心无微不至,其中对我们物质帮助是最重要的一个指标,下表是一个统计员在统计《父母为我花了多少》当中使用处理得到下列的数据:
参考数据公式: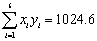 ,
,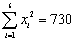 ,
,
线性回归方程: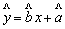 ,(
,(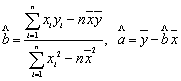 )
)
| 岁数 | 1 | 2 | 6 | 12 | 16 | 17 |
| 花费累积 | 1 | 2.8 | 9 | 17 | 22 | 24 |
假设花费累积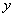 与岁数
与岁数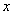 符合线性相关关系,求
符合线性相关关系,求
(1)花费累积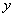 与岁数
与岁数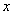 的线性回归直线方程(系数保留3位小数);
的线性回归直线方程(系数保留3位小数);
(2)24岁大学毕业之后,我们不再花父母的钱,假设你在30岁成家立业之后,在你50岁之前偿还父母为你的花费(不计利息)。那么你每月要偿还父母约多少元钱?
查看答案和解析>>
科目:高中数学 来源: 题型:
某产品的广告费用x与销售额y的统计数据如下表
广告费用x(万元) 4 2 3 5
销售额y(万元) 49 26 39 54
根据上表可得回归方程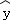 =
=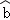 x+
x+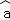 的
的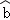 为9.4,据此模型预报广告费用为6万元时销售额为()
为9.4,据此模型预报广告费用为6万元时销售额为()
A. 63.6万元 B. 65.5万元 C. 67.7万元 D. 72.0万元
查看答案和解析>>
科目:高中数学 来源: 题型:
数列1,(1+2),(1+2+22),…,(1+2+22+…+2n﹣1)…的前n项和为()
A. 2n﹣1 B. n•2n﹣n C. 2n+1﹣n D. 2n+1﹣2﹣n
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com