
某地区2003年年底的绿化面积为95万公顷,之后五年采取了退耕还林、植树造林的措施,该地区的绿化情况如下表所示:
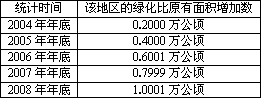
若继续采取这项植树造林的措施,那么到2018年年底,该地区的绿化面积将大约变为多少万公顷?
|
分析:本题不能直接看出题中涉及的是哪种函数类型,故只能先抓住题中所给的一些数据画出散点图观察,然后通过函数模型与数据拟合的方法确定函数关系.
解:设2004年至2008年分别为第1,2,3,4,5年,则由上表数据可画出表示绿化面积增加数y与年份编号x之间关系的散点图. 通过观察发现,y与x关系的图象近似于一条直线,所以y与x的关系可用一次函数表示,设y=kx+b,由 因为该地区的原有绿化面积为95万公顷,所以,到2018年年底绿化面积大约变为95+0.2×15=98万公顷. 点评:本解实际上是建立函数模型的一种最简单的情形:(1)根据原始数据画出散点图;(2)观察散点图,拟合函数;(3)求出函数解析式;(4)根据条件验证作答. |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com