

思路分析:据题设知,单位距离的公路运费大于铁路运费,又知|BD|+|DC|≤|BA|+|AC|,因此只有点D选在线段BA上某一适当位置,才能使总运费最省.若设D点距A点x千米,从B到C的总动费为y,建立y与x的函数,则通过函数y=f(x)的最小值,可确定点D的位置.
解:设|DA|=x(千米),铁路每吨千米运费
y=![]() ,x∈(0,100),
,x∈(0,100),
即![]() =5
=5![]() -3x.
-3x.
令t=![]() ,则有t+3x=5
,则有t+3x=5![]() .
.
平方、整理,得16x2-6tx+10000-t2=0.①
由①36t2-4×16(10000-t2)≥0,得|t|≥80.
∵t>0,∴t≥80.
将t=80代入方程①,得x=15,这时t最小,y也最小.
故当D点选在距A点


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:高中数学 来源:江苏省徐州市丰县修远双语学校2011-2012学年高二上学期第二次月考数学试题 题型:044
如图,l1、l2是通过某城市开发区中心O的两条南北和东西走向的街道,连接M、N两地之间的铁路线是圆心在l2上的一段圆弧.若点M在点O正北方向,且|MO|=3 km,点N到l1、l2的距离分别为4 km和5 km.
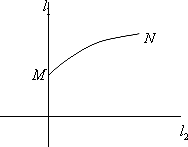
(1)建立适当坐标系,求铁路线所在圆弧的方程;
(2)若该城市的某中学拟在点O正东方向选址建分校,考虑环境问题,要求校址到点O的距离大于4 km,并且铁路线上任意一点到校址的距离不能少于![]() km,求该校址距点O的最近距离(注:校址视为一个点).
km,求该校址距点O的最近距离(注:校址视为一个点).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com