
【题目】已知函数![]() ,证明:
,证明:
(1)![]() 在区间
在区间![]() 存在唯一极大值点;
存在唯一极大值点;
(2)![]() 有且仅有2个零点.
有且仅有2个零点.
【答案】(1)证明见解析(2)证明见解析
【解析】
(1)设![]() ,对
,对![]() 求导可知
求导可知![]() 在
在![]() 上单调递减,利用零点存在性定理可得
上单调递减,利用零点存在性定理可得![]() 在
在![]() 上有唯一的零点
上有唯一的零点![]() ,进而求证即可;
,进而求证即可;
(2)利用导函数分别讨论![]() ,
,![]() ,
,![]() 的单调性,判断函数图象的性质,进而求证即可.
的单调性,判断函数图象的性质,进而求证即可.
证明:(1)设![]() ,
,
当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递减,
上单调递减,
又因为![]() ,
,![]() ,
,
所以![]() 在
在![]() 上有唯一的零点
上有唯一的零点![]() ,
,
即函数![]() 在
在![]() 上存在唯一零点,
上存在唯一零点,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() 在
在![]() 上存在唯一的极大值点
上存在唯一的极大值点![]()
(2)①由(1)知:![]() 在
在![]() 上存在唯一的极大值点
上存在唯一的极大值点![]() ,
,
所以![]() ,
,
又因为![]() ,
,
所以![]() 在
在![]() 上恰有一个零点,
上恰有一个零点,
又因为![]() ,
,
所以![]() 在
在![]() 上也恰有一个零点,
上也恰有一个零点,
②当![]() 时,
时,![]() ,
,![]() ,
,
设![]() ,
,![]() ,
,
所以![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,
,
所以当![]() 时,
时,![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上没有零点,
上没有零点,
③当![]() 时,
时,![]() ,
,
设![]() ,
,![]() ,
,
所以![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,
,
所以当![]() 时,
时,![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上没有零点,
上没有零点,
综上,![]() 有且仅有两个零点.
有且仅有两个零点.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,过点
,过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 两点,延长
两点,延长![]() 交椭圆
交椭圆![]() 于点
于点![]() ,
,![]() 的周长为8.
的周长为8.

(1)求![]() 的离心率及方程;
的离心率及方程;
(2)试问:是否存在定点![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() .
.
(1)若数列![]() 是等差数列,且
是等差数列,且![]() ,求实数
,求实数![]() 的值;
的值;
(2)若数列![]() 满足
满足![]()
![]() ,且
,且![]() ,求证:数列
,求证:数列![]() 是等差数列;
是等差数列;
(3)设数列![]() 是等比数列,试探究当正实数
是等比数列,试探究当正实数![]() 满足什么条件时,数列
满足什么条件时,数列![]() 具有如下性质
具有如下性质![]() :对于任意的
:对于任意的![]()
![]() ,都存在
,都存在![]() 使得
使得![]() ,写出你的探求过程,并求出满足条件的正实数
,写出你的探求过程,并求出满足条件的正实数![]() 的集合.
的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年5月20日以来,广东自西北到东南出现了一次明显降雨.为了对某地的降雨情况进行统计,气象部门对当地20日~28日9天记录了其中100小时的降雨情况,得到每小时降雨情况的频率分布直方图如下:

若根据往年防汛经验,每小时降雨量在![]() 时,要保持二级警戒,每小时降雨量在
时,要保持二级警戒,每小时降雨量在![]() 时,要保持一级警戒.
时,要保持一级警戒.
(1)若从记录的这100小时中按照警戒级别采用分层抽样的方法抽取10小时进行深度分析.
①求一级警戒和二级警戒各抽取多少小时;
②若从这10个小时中任选2个小时,则这2个小时中恰好有1小时属于一级警戒的概率.(2)若以每组的中点代表该组数据值,求这100小时内的平均降雨量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1为某省2018年1~4月快递业务量统计图,图2是该省2018年1~4月快递业务收入统计图,下列对统计图理解错误的是( )


A. 2018年1~4月的业务量,3月最高,2月最低,差值接近2000万件
B. 2018年1~4月的业务量同比增长率均超过50%,在3月底最高
C. 从两图来看,2018年1~4月中的同一个月的快递业务量与收入的同比增长率并不完全一致
D. 从1~4月来看,该省在2018年快递业务收入同比增长率逐月增长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,椭圆上动点
,椭圆上动点![]() 到点
到点![]() 的最远距离和最近距离分别为
的最远距离和最近距离分别为![]() 和
和![]() .
.
(1)求椭圆的方程;
(2)设![]() 分别为椭圆的左、右顶点,过点
分别为椭圆的左、右顶点,过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 、
、![]() 两点,若
两点,若![]() ,
,![]() 为坐标原点,求
为坐标原点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
如图,在直三棱柱![]() 中,平面
中,平面![]() 侧面A1ABB1.
侧面A1ABB1.
(Ⅰ)求证:![]() ;
;
(Ⅱ)若直线AC与平面A1BC所成的角为θ,二面角A1-BC-A的大小为φ,试判断θ与φ的大小关系,并予以证明.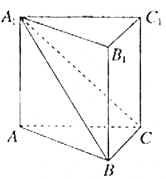
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年全国数学奥赛试行改革:在高二一年中举行5次全区竞赛,学生如果其中2次成绩达全区前20名即可进入省队培训,不用参加其余的竞赛,而每个学生最多也只能参加5次竞赛.规定:若前4次竞赛成绩都没有达全区前20名,则第5次不能参加竞赛.假设某学生每次成绩达全区前20名的概率都是![]() ,每次竞赛成绩达全区前20名与否互相独立.
,每次竞赛成绩达全区前20名与否互相独立.
(1)求该学生进入省队的概率.
(2)如果该学生进入省队或参加完5次竞赛就结束,记该学生参加竞赛的次数为![]() ,求
,求![]() 的分布列及
的分布列及![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 所在的平面和平面
所在的平面和平面![]() 互相垂直,等腰梯形
互相垂直,等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() 为底面
为底面![]() 的重心.
的重心.
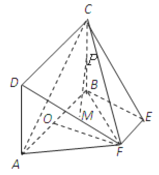
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com