
【题目】
如图,在直三棱柱![]() 中,平面
中,平面![]() 侧面A1ABB1.
侧面A1ABB1.
(Ⅰ)求证:![]() ;
;
(Ⅱ)若直线AC与平面A1BC所成的角为θ,二面角A1-BC-A的大小为φ,试判断θ与φ的大小关系,并予以证明.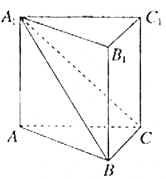
【答案】(Ⅰ)证明见解析.
(Ⅱ)![]() ,证明见解析.
,证明见解析.
【解析】
(Ⅰ)证明:如右图,过点A在平面A1ABB1内作AD⊥A1B于D,则
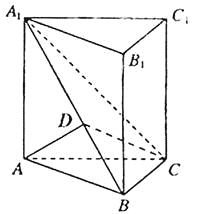
由平面A1BC⊥侧面A1ABB1,且平面A1BC![]() 侧面A1ABB1=A1B,得
侧面A1ABB1=A1B,得
AD⊥平面A1BC,又BC![]() 平面A1BC,所以AD⊥BC.
平面A1BC,所以AD⊥BC.
因为三棱柱ABC—A1B1C1是直三棱柱,则AA1⊥底面ABC,所以AA1⊥BC.
又AA1![]() AD=A,从而BC⊥侧面A1ABB1,
AD=A,从而BC⊥侧面A1ABB1,
又AB![]() 侧面A1ABB1,故AB⊥BC.
侧面A1ABB1,故AB⊥BC.
(Ⅱ)解法1:连接CD,则由(Ⅰ)知![]() 是直线AC与平面A1BC所成的角,
是直线AC与平面A1BC所成的角,
![]() 是二面角A1—BC—A的平面角,即
是二面角A1—BC—A的平面角,即![]()
于是在![]() 中,
中,![]() 在
在![]() 中,
中,![]() ,
,
由![]() ,得
,得![]() ,又
,又![]() ,所以
,所以![]() .
.
解法2:由(1)知,以点![]() 为坐标原点,以
为坐标原点,以![]() 、
、![]() 、
、![]() 所在的直线分
所在的直线分![]() 轴、
轴、![]() 轴、
轴、![]() 轴,建立如图所示的空间直角坐标系,
轴,建立如图所示的空间直角坐标系,

设![]() ,
,
则![]() ,
,
于是![]() ,
,![]() .
.
设平面的一个法向量为![]() ,则
,则
由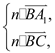 得
得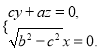
可取![]() ,于是
,于是![]() 与
与![]() 的夹角
的夹角![]() 为锐角,则
为锐角,则![]() 与
与![]() 互为余角.
互为余角.
所以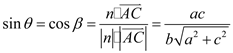 ,
,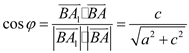 ,
,
所以![]() .
.
于是由![]() ,得
,得![]() ,
,
即![]() ,又
,又![]() 所以
所以![]() .
.
第(1)问证明线线垂直,一般先证线面垂直,再由线面垂直得线线垂直;第(2)问若用传统方法一般来说要先作垂直,进而得直角三角形.若用向量方法,关键在求法向量.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左焦点为
的左焦点为![]() ,下顶点为
,下顶点为![]() ,上顶点为
,上顶点为![]() ,
,![]() 是等边三角形.
是等边三角形.
(Ⅰ)求椭圆的离心率;
(Ⅱ)设直线![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线与椭圆交于点
的直线与椭圆交于点![]()
![]() 异于点
异于点![]() ,线段
,线段![]() 的垂直平分线与直线
的垂直平分线与直线![]() 交于点
交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,若
,若![]() .
.
(ⅰ)求![]() 的值;
的值;
(ⅱ)已知点![]() ,点
,点![]() 在椭圆上,若四边形
在椭圆上,若四边形![]() 为平行四边形,求椭圆的方程.
为平行四边形,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,且
,且![]() 在椭圆
在椭圆![]() 上运动,当点
上运动,当点![]() 恰好在直线l:
恰好在直线l:![]() 上时,
上时,![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)作与![]() 平行的直线
平行的直线![]() ,与椭圆交于
,与椭圆交于![]() 两点,且线段
两点,且线段![]() 的中点为
的中点为![]() ,若
,若![]() 的斜率分别为
的斜率分别为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,函数
,函数![]() 在
在![]() ,
,![]() 处取得极值,其中
处取得极值,其中![]() .
.
(1)求实数t的取值范围;
(2)判断![]() 在
在![]() 上的单调性并证明;
上的单调性并证明;
(3)已知![]() 在
在![]() 上的任意
上的任意![]() 、
、![]() ,都有
,都有![]() ,令
,令![]() ,若函数
,若函数![]() 有3个不同的零点,求实数m的取值范围.
有3个不同的零点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2010-2018年之间,受益于基础设施建设对光纤产品的需求,以及个人计算机及智能手机的下一代规格升级,电动汽车及物联网等新机遇,连接器行业增长呈现加速状态.根据该折线图,下列结论正确的个数为( )

①每年市场规模量逐年增加;
②增长最快的一年为2013~2014;
③这8年的增长率约为40%;
④2014年至2018年每年的市场规模相对于2010年至2014年每年的市场规模,数据方差更小,变化比较平稳
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人准备投资1200万元办一所中学,为了考虑社会效益和经济效益,对该地区教育市场进行调查,得出一组数据,列表如下(以班级为单位).
市场调查表:
班级学生数 | 配备教师数 | 硬件建设费(万元) | 教师年薪(万元) | |
初中 | 50 | 2.0 | 28 | 1.2 |
高中 | 40 | 2.5 | 58 | 1.6 |
根据物价部门的有关规定:初中是义务教育阶段,收费标准适当控制,预计除书本费、办公费外,初中每人每年可收取600元.高中每人每年可收取1500元.因生源和环境等条件限制,办学规模以20至30个班为宜(含20个班与30个),教师实行聘任制.初、高中教育周期均为三年,设初中编制为![]() 个班,高中编制为
个班,高中编制为![]() 个班,请你合理地安排招生计划,使年利润最大.
个班,请你合理地安排招生计划,使年利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 1(a>b>0)的左右焦点分别为F1F2,左右顶点分别为AB,上顶点为T,且△TF1F2为等边三角形.
1(a>b>0)的左右焦点分别为F1F2,左右顶点分别为AB,上顶点为T,且△TF1F2为等边三角形.
(1)求此椭圆的离心率e;
(2)若直线y=kx+m(k>0)与椭圆交与CD两点(点D在x轴上方),且与线段F1F2及椭圆短轴分别交于点MN(其中MN不重合),且|CM|=|DN|.
①求k的值;
②设ADBC的斜率分别为k1,k2,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com