
【题目】已知椭圆![]() 1(a>b>0)的左右焦点分别为F1F2,左右顶点分别为AB,上顶点为T,且△TF1F2为等边三角形.
1(a>b>0)的左右焦点分别为F1F2,左右顶点分别为AB,上顶点为T,且△TF1F2为等边三角形.
(1)求此椭圆的离心率e;
(2)若直线y=kx+m(k>0)与椭圆交与CD两点(点D在x轴上方),且与线段F1F2及椭圆短轴分别交于点MN(其中MN不重合),且|CM|=|DN|.
①求k的值;
②设ADBC的斜率分别为k1,k2,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() .(2)①
.(2)①![]() ,②
,②![]()
【解析】
(1)设![]() 的半焦距为c,由题得a=2c,即得椭圆的离心率;(2)①设C(x1,y1),D(x2,y2),联立直线和椭圆方程得到
的半焦距为c,由题得a=2c,即得椭圆的离心率;(2)①设C(x1,y1),D(x2,y2),联立直线和椭圆方程得到![]() ,化简即得解;②先分析得到
,化简即得解;②先分析得到![]() ,求出
,求出![]() ,进一步分析得到
,进一步分析得到![]() 的取值范围.
的取值范围.
(1)设![]() 的半焦距为c,
的半焦距为c,
由△TF1F2为等边三角形.得a=2c,
即椭圆的离心率![]() ;
;
(2)①设C(x1,y1),D(x2,y2),由y=kx+m,可知![]() ,N(0,m),
,N(0,m),
联立y=kx+m与![]() ,整理得(a2k2+b2)x2+2kma2x+a2m2﹣a2b2=0,
,整理得(a2k2+b2)x2+2kma2x+a2m2﹣a2b2=0,
其中△=4a2b2(a2k2+b2﹣m2)>0,
易知,x1+x2=xM+xN,即![]() ,
,
解得![]() ,
,
因为,k>0,所以![]() ,
,
②由M在线段F1F2,且M,N不重合,
可知,![]() ,
,
从而![]() ,
,
即![]() ,
,![]() ,并结合在曲线上,则有,
,并结合在曲线上,则有,
所以![]() ,
,
从而可得,![]() ∈
∈![]() ,
,
所以![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】
如图,在直三棱柱![]() 中,平面
中,平面![]() 侧面A1ABB1.
侧面A1ABB1.
(Ⅰ)求证:![]() ;
;
(Ⅱ)若直线AC与平面A1BC所成的角为θ,二面角A1-BC-A的大小为φ,试判断θ与φ的大小关系,并予以证明.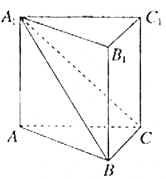
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小学举办“父母养育我,我报父母恩”的活动,对六个年级(一年级到六年级的年级代码分别为1,2…,6)的学生给父母洗脚的百分比y%进行了调查统计,绘制得到下面的散点图.
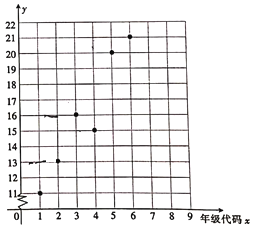
(1)由散点图看出,可用线性回归模型拟合y与x的关系,请用相关系数加以说明;
(2)建立y关于x的回归方程,并据此预计该校学生升入中学的第一年(年级代码为7)给父母洗脚的百分比.
附注:参考数据:![]()
参考公式:相关系数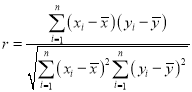 ,若r>0.95,则y与x的线性相关程度相当高,可用线性回归模型拟合y与x的关系.回归方程
,若r>0.95,则y与x的线性相关程度相当高,可用线性回归模型拟合y与x的关系.回归方程![]() 中斜率与截距的最小二乘估计公式分别为
中斜率与截距的最小二乘估计公式分别为![]() =
=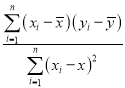 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 所在的平面和平面
所在的平面和平面![]() 互相垂直,等腰梯形
互相垂直,等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() 为底面
为底面![]() 的重心.
的重心.
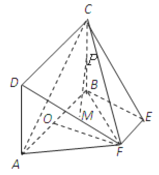
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂销售部以箱为单位销售某种零件,每箱的定价为200元,低于100箱按原价销售;不低于100箱通过双方议价,买方能以优惠![]() 成交的概率为0.6,以优惠
成交的概率为0.6,以优惠![]() 成交的概率为0.4.
成交的概率为0.4.
(1)甲、乙两单位都要在该厂购买150箱这种零件,两单位各自达成的成交价相互独立,求甲单位优惠比例不低于乙单位优惠比例的概率;
(2)某单位需要这种零件650箱,求购买总价![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
B.命题“若![]() ,则
,则![]() ”的逆否命题为:“若
”的逆否命题为:“若![]() ,则
,则![]() ”
”
C.若![]() 为假命题,则
为假命题,则![]() ,
,![]() 均为假命题
均为假命题
D.命题![]() ,使得
,使得![]() ,则
,则![]() ,使得
,使得![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂过去在生产过程中将污水直接排放到河流中对沿河环境造成了一定的污染,根据环保部门对该厂过去10年的监测数据,统计出了其每年污水排放量![]() (单位:吨)的频率分布表:
(单位:吨)的频率分布表:
污水排放量 |
|
|
|
|
频率 | 0.1 | 0.3 | 0.4 | 0.2 |
将污水排放量落入各组的频率作为概率,并假设每年该厂污水排放量相互独立.
(1)若不加以治理,根据上表中的数据,计算未来3年中至少有2年污水排放量不小于200吨的概率;
(2)根据环保部门的评估,该厂当年污水排放量![]() 时,对沿河环境及经济造成的损失为5万元;当年污水排放量
时,对沿河环境及经济造成的损失为5万元;当年污水排放量![]() 时,对沿河环境及经济造成的损失为10万元;当年污水排放量
时,对沿河环境及经济造成的损失为10万元;当年污水排放量![]() 时,对沿河环境及经济造成的损失为20万元;当年污水排放量
时,对沿河环境及经济造成的损失为20万元;当年污水排放量![]() 时,对沿河环境及经济造成的损失为50万元.为了保护环境,减少损失,该厂现有两种应对方案:
时,对沿河环境及经济造成的损失为50万元.为了保护环境,减少损失,该厂现有两种应对方案:
方案1:若该厂不采取治污措施,则需全部赔偿对沿河环境及经济造成的损失;
方案2:若该厂采购治污设备对所有产生的污水净化达标后再排放,则不需赔偿,采购设备的费用为10万元,每年设备维护等费用为15万元,该设备使用10年需重新更换.在接下来的10年里,试比较上述2种方案哪种能为该厂节约资金,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某包子店每天早晨会提前做好若干笼包子,以保证当天及时供应,每卖出一笼包子的利润为40元,当天未卖出的包子作废料处理, 每笼亏损20元.该包子店记录了60天包子的日需求量![]() (单位:笼,
(单位:笼,![]() ),整理得到如图所示的条形图,以这60天各需求量的频率代替相应的概率.
),整理得到如图所示的条形图,以这60天各需求量的频率代替相应的概率.
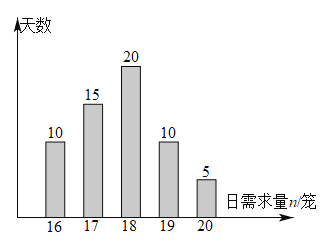
(1)设![]() 为一天的包子需求量,求
为一天的包子需求量,求![]() 的数学期望.
的数学期望.
(2)若该包子店想保证![]() 以上的天数能够足量供应,则每天至少要做多少笼包子?
以上的天数能够足量供应,则每天至少要做多少笼包子?
(3)为了减少浪费,该包子店一天只做18笼包子,设![]() 为当天的利润(单位:元),求
为当天的利润(单位:元),求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com