
【题目】下列说法错误的是( )
A.“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
B.命题“若![]() ,则
,则![]() ”的逆否命题为:“若
”的逆否命题为:“若![]() ,则
,则![]() ”
”
C.若![]() 为假命题,则
为假命题,则![]() ,
,![]() 均为假命题
均为假命题
D.命题![]() ,使得
,使得![]() ,则
,则![]() ,使得
,使得![]()
 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,函数
,函数![]() 在
在![]() ,
,![]() 处取得极值,其中
处取得极值,其中![]() .
.
(1)求实数t的取值范围;
(2)判断![]() 在
在![]() 上的单调性并证明;
上的单调性并证明;
(3)已知![]() 在
在![]() 上的任意
上的任意![]() 、
、![]() ,都有
,都有![]() ,令
,令![]() ,若函数
,若函数![]() 有3个不同的零点,求实数m的取值范围.
有3个不同的零点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“割圆术”是刘徽最突出的数学成就之一,他在《九章算术注》中提出割圆术,并作为计算圆的周长,面积已经圆周率的基础,刘徽把圆内接正多边形的面积一直算到了正3072边形,并由此而求得了圆周率为3.1415和3.1416这两个近似数值,这个结果是当时世界上圆周率计算的最精确数据.如图,当分割到圆内接正六边形时,某同学利用计算机随机模拟法向圆内随机投掷点,计算得出该点落在正六边形内的频率为0.8269,那么通过该实验计算出来的圆周率近似值为(参考数据:![]() )
)

A. 3.1419B. 3.1417C. 3.1415D. 3.1413
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 和圆
和圆![]() ,倾斜角为45°的直线
,倾斜角为45°的直线![]() 过抛物线
过抛物线![]() 的焦点,且
的焦点,且![]() 与圆
与圆![]() 相切.
相切.
(1)求![]() 的值;
的值;
(2)动点![]() 在抛物线
在抛物线![]() 的准线上,动点
的准线上,动点![]() 在
在![]() 上,若
上,若![]() 在
在![]() 点处的切线
点处的切线![]() 交
交![]() 轴于点
轴于点![]() ,设
,设![]() .求证点
.求证点![]() 在定直线上,并求该定直线的方程.
在定直线上,并求该定直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 1(a>b>0)的左右焦点分别为F1F2,左右顶点分别为AB,上顶点为T,且△TF1F2为等边三角形.
1(a>b>0)的左右焦点分别为F1F2,左右顶点分别为AB,上顶点为T,且△TF1F2为等边三角形.
(1)求此椭圆的离心率e;
(2)若直线y=kx+m(k>0)与椭圆交与CD两点(点D在x轴上方),且与线段F1F2及椭圆短轴分别交于点MN(其中MN不重合),且|CM|=|DN|.
①求k的值;
②设ADBC的斜率分别为k1,k2,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线l的参数方程为
中,直线l的参数方程为![]() (t为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]()
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)若直线l与曲线C相交于A,B两点.求![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,其中,频率分布直方图的分组区间分别为![]() ,据此解答如下问题.
,据此解答如下问题.
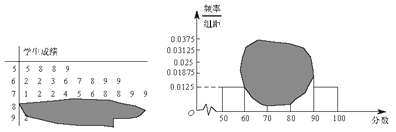
(Ⅰ)求全班人数及分数在![]() 之间的频率;
之间的频率;
(Ⅱ)现从分数在![]() 之间的试卷中任取 3 份分析学生情况,设抽取的试卷分数在
之间的试卷中任取 3 份分析学生情况,设抽取的试卷分数在![]() 的份数为
的份数为![]() ,求
,求![]() 的分布列和数学望期.
的分布列和数学望期.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com