
【题目】首项为正数的数列{an}满足an+1=(a+3),n∈N*.
(1)证明:若a1为奇数,则对一切n≥2,an都是奇数;
(2)若对一切n∈N*都有an+1>an , 求a1的取值范围.
【答案】
(1)
【解答】
证明:已知a1是奇数,假设ak=2m-1是奇数,其中m为正整数,则由递推关系得![]() 是奇数.
是奇数.
根据数学归纳法,对任意n∈N*,an都是奇数
(2)
【解答】
由an+1-an=![]() (an-1)(an-3)知
(an-1)(an-3)知
当且仅当an<1或an>3时,an+1>an,
另一方面,若0<ak<1,
则0<ak+1<![]() =1;
=1;
若ak>3,则ak+1>![]() .
.
根据数学归纳法可知,![]()
![]()
综上所述,对一切n∈N*,都有an+1>an的充要条件是0<a1<1或a1>3.
【解析】一般地,证明一个与正整数n有关的命题,可按下列步骤进行:(1)(归纳奠基)证明当n取第一个值时命题成立;(2)(归纳递推)假设n=k(k≥n0,k∈N+)时命题成立,证明当n=k+1时命题也成立.
只要完成这两个步骤,就可以断定命题对从n0开始的所有正整数n都成立.上述证明方法叫做数学归纳法
【考点精析】根据题目的已知条件,利用数学归纳法的步骤的相关知识可以得到问题的答案,需要掌握
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某蛋糕店出售一种蛋糕,这种蛋糕的保质期很短,必须当天卖掉,否则容易变质,该蛋糕店每天以每块16元的成本价格制作这种蛋糕若干块,然后以每块26元的价格出售,如果当天卖不完,剩下的蛋糕只能以每块6元低价出售.蛋糕店记录了100天该种蛋糕的日需求量n(单位:块,n∈N*)整理得如图: 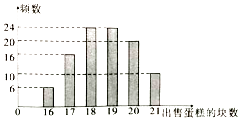
(1)若该蛋糕店某一天制作19块蛋糕,求当天的利润y(单位:元)关于当天需求量n的函数解析式;
(2)若要求出售“出售的蛋糕块数不小于n”的频率不小于0.4,求n的最大值.
(3)若该蛋糕店这100天每天都制作19块蛋糕,试计算这100天蛋糕店所获利润的平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校制定学校发展规划时,对现有教师进行年龄状况和接受教育程度(学历)的调查,其结果(人数分布)如表:
学历 | 35岁以下 | 35至50岁 | 50岁以上 |
本科 | 80 | 30 | 20 |
研究生 | x | 20 | y |
(Ⅰ)用分层抽样的方法在35至50岁年龄段的教师中抽取一个容量为5的样本,将该样本看成一个总体,从中任取2人,求至少有l人的学历为研究生的概率;
(Ⅱ)在该校教师中按年龄状况用分层抽样的方法抽取N个人,其中35岁以下48人,50岁以上10人,再从这N个人中随机抽取l人,此人的年龄为50岁以上的概率为 ![]() ,求x、y的值.
,求x、y的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点Pn(an , bn)满足an+1=an·bn+1 , bn+1=(n∈N*)且点P1的坐标为(1,-1).
(1)求过点P1 , P2的直线l的方程;
(2)试用数学归纳法证明:对于n∈N* , 点Pn都在(1)中的直线l上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=f(x)是定义在a,b上的增函数,其中a,b∈R且0<b<﹣a,已知y=f(x)无零点,设函数F(x)=f2(x)+f2(﹣x),则对于F(x)有以下四个说法:
①定义域是[﹣b,b];②是偶函数;③最小值是0;④在定义域内单调递增.
其中正确的有(填入你认为正确的所有序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com