
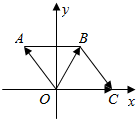
 如图已知四边形AOCB中,|$\overrightarrow{OA}$|=5,$\overrightarrow{OC}$=(5,0),点B位于第一象限,若△BOC为正三角形.
如图已知四边形AOCB中,|$\overrightarrow{OA}$|=5,$\overrightarrow{OC}$=(5,0),点B位于第一象限,若△BOC为正三角形.分析 (1)设∠AOB=α,cosα=$\frac{3}{5}$,sinα=$\frac{4}{5}$.可得:xA=$5cos(α+\frac{π}{3})$,yA=$5sin(α+\frac{π}{3})$.
(2)B$(\frac{5}{2},\frac{5\sqrt{3}}{2})$,计算$\overrightarrow{OA}•\overrightarrow{BC}$.$|\overrightarrow{OA}|$,$|\overrightarrow{BC}|$.可得cosθ=$\frac{\overrightarrow{OA}•\overrightarrow{BC}}{|\overrightarrow{OA}||\overrightarrow{BC}|}$.
解答 解:(1)设∠AOB=α,cosα=$\frac{3}{5}$,sinα=$\frac{4}{5}$.
xA=$5cos(α+\frac{π}{3})$=$5(\frac{3}{5}×\frac{1}{2}-\frac{4}{5}×\frac{\sqrt{3}}{2})$=$\frac{3-4\sqrt{3}}{2}$.
yA=$5sin(α+\frac{π}{3})$=5$(\frac{4}{5}×\frac{1}{2}+\frac{3}{5}×\frac{\sqrt{3}}{2})$=$\frac{4+3\sqrt{3}}{2}$.
∴A$(\frac{3-4\sqrt{3}}{2},\frac{4+3\sqrt{3}}{2})$.
(2)B$(\frac{5}{2},\frac{5\sqrt{3}}{2})$,
$\overrightarrow{BC}$=$(\frac{5}{2},-\frac{5\sqrt{3}}{2})$.
$\overrightarrow{OA}$=$(\frac{3-4\sqrt{3}}{2},\frac{4+3\sqrt{3}}{2})$.
∴$\overrightarrow{OA}•\overrightarrow{BC}$=$\frac{15-20\sqrt{3}}{4}$-$\frac{20\sqrt{3}+45}{4}$=$-\frac{15+20\sqrt{3}}{2}$.
$|\overrightarrow{OA}|$=5,$|\overrightarrow{BC}|$=5.
∴cosθ=$\frac{\overrightarrow{OA}•\overrightarrow{BC}}{|\overrightarrow{OA}||\overrightarrow{BC}|}$=$-\frac{3+4\sqrt{3}}{10}$.
∴cos2θ=2cos2θ-1=$\frac{7+24\sqrt{3}}{50}$.
点评 本题考查了向量的坐标运算、数量积运算性质、向量夹角公式,考查了推理能力与计算能力,属于中档题.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
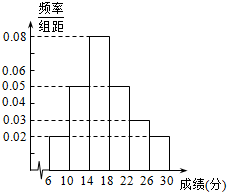 为了解某省去年高三考生英语听力成绩,现从某校高三年级随机抽取50名考生的成绩,发现全部介于[6,30]之间,将成绩按如下方式分成6组:第1组[6,10),第2组[10,14),…,第6组[26,30],如图是按上述分组方法得到的频率分布直方图.
为了解某省去年高三考生英语听力成绩,现从某校高三年级随机抽取50名考生的成绩,发现全部介于[6,30]之间,将成绩按如下方式分成6组:第1组[6,10),第2组[10,14),…,第6组[26,30],如图是按上述分组方法得到的频率分布直方图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com