
-2<m<8 7
分析:A 把参数方程、极坐标方程化为普通方程,利用点到直线的距离公式及弦长公式求得弦长.
B 有绝对值的意义知,|x-3|+|x-m|的最小值为|m-3|,故|m-3|<5,去掉绝对值求得m范围.
C 如图:由题意得,三角形的内切圆半径等于1,外接圆的半径等于3,设A(a,0),B(0,b),a>0,b>0,
点C(1,1)为△AOB的内心,由点C到AB的距离等于1,及

=6,解方程求得 ab,即可求得
三角形的面积

ab 的值.
解答:A 用代入法消去参数,化为普通的直线方程为 3x-4y-8=0,利用同角三角函数的基本关系
消去参数θ得到曲线的普通方程为 (x-5)
2+(y-3)
2=4,表示圆心在(5,3),半径等于2的圆.
圆心到直线的距离等于
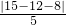
=1,故弦长为 2
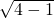
=2

.
B 由于|x-3|+|x-m|表示数轴上的x 到3和m的距离之和,故其最小值为|m-3|,
∵存在实数x满足|x-3|+|x-m|<5,∴|m-3|<5,-5<m-3<5,-2<m<8.
C 由题意得,三角形的内切圆半径等于1,外接圆的半径等于3,直角三角形的斜边中点到三个顶点的距离相等,
故直角三角形的斜边长等于6,如图:设A(a,0),B(0,b),a>0,b>0,
Rt△AOB中,点C(1,1)为△AOB的内心,AB的中点D是△AOB的外心.
,

=6=AB,AB的方程为

,即 bx+ay-ab=0.
由题意知,点C到AB的距离等于1,∴

=1,∴|b+a-ab|=6,
b+a-ab=6 ①,b+a-ab=-6 ②.
把①移向平方得 a
2+b
2+2ab=(ab)
2+12ab+36,∴ab=0(舍去),或 ab=-10(舍去),
把②移向平方得 a
2+b
2+2ab=(ab)
2-12ab+36,∴ab=0(舍去) 或 ab=14,
故三角形的面积为

ab=7.
故答案为 A 2

; B-2<m<8; C 7.

,
点评:本题考查把参数方程、极坐标方程化为普通方程的方法,绝对值不等式的解法,点到直线的距离公式的
应用.

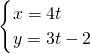 (t为参数)被曲线
(t为参数)被曲线 (θ为参数)所截得的弦长为________;
(θ为参数)所截得的弦长为________; -2<m<8 7
-2<m<8 7 =6,解方程求得 ab,即可求得
=6,解方程求得 ab,即可求得 ab 的值.
ab 的值.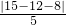 =1,故弦长为 2
=1,故弦长为 2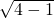 =2
=2 .
. =6=AB,AB的方程为
=6=AB,AB的方程为  ,即 bx+ay-ab=0.
,即 bx+ay-ab=0.  =1,∴|b+a-ab|=6,
=1,∴|b+a-ab|=6, ab=7.
ab=7. ; B-2<m<8; C 7.
; B-2<m<8; C 7. ,
,

 满足
满足 ,则
,则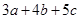 的最大值为_________.
的最大值为_________. 的直角边
的直角边 为直径的圆
为直径的圆 交
交 边于点
边于点 ,点
,点 在
在 上,且
上,且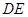 与圆
与圆 相切.若
相切.若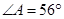 ,则
,则 _________.
_________. 与直线
与直线 的两个交点之间的距离为_________.
的两个交点之间的距离为_________. 满足
满足 ,则
,则 的最大值为_________.
的最大值为_________. 的直角边
的直角边 为直径的圆
为直径的圆 交
交 边于点
边于点 ,点
,点 在
在 上,且
上,且 与圆
与圆 相切.若
相切.若 ,则
,则 _________.
_________. 与直线
与直线 的两个交点之间的距离为_________.
的两个交点之间的距离为_________.