解:(1)由sin
2C=sin
2A+sin
2B+sinA•sinB,
利用正弦定理化简得:c
2=a
2+b
2+ab(*),
则根据余弦定理得:cosC=

=-

,由C∈(0,180°),
得到:C=120°;
(2)∵c=2RsinC=2

,又

absinC=

,∴ab=4,
把c的值代入(*)得:12=a
2+b
2+ab=(a+b)
2-ab,
∴(a+b)
2=16,
则a+b=4.
分析:(1)根据正弦定理化简已知的等式得到一个关系式,记作(*),然后利用余弦定理表示出cosC,把(*)代入即可求出cosC的值,然后由C的范围,利用特殊角的三角函数值即可求出C的度数;
(2)由(1)求出的C的度数求出sinC的值,然后由sinC的值,利用△ABC的面积公式求出ab的值,又△ABC的外接圆半径是2,根据正弦定理求出c的值,代入(*)化简,配方后把ab的值代入即可求出a+b的值.
点评:解本题的关键是利用正弦定理化简已知的等式.综合考查了正弦定理、余弦定理以及三角形的面积公式解决数学问题.本题的综合性比较强,要求学生掌握知识全面.

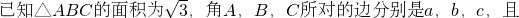 sin2C=sin2A+sin2B+sinA•sinB,
sin2C=sin2A+sin2B+sinA•sinB, =-
=- ,由C∈(0,180°),
,由C∈(0,180°), ,又
,又 absinC=
absinC= ,∴ab=4,
,∴ab=4,

 全能练考卷系列答案
全能练考卷系列答案