
(12分) 将直线![]() 绕着它与
绕着它与![]() 轴的交点按逆时针方向旋转
轴的交点按逆时针方向旋转![]() 角后,恰好与圆
角后,恰好与圆![]()
![]() 相切,求旋转角
相切,求旋转角![]() 的最小值.
的最小值.
科目:高中数学 来源: 题型:
(本题满分12分,第(1)小题6分,第(2)小题6分)
如图,![]() 是圆柱体
是圆柱体![]() 的一条母线,
的一条母线,![]() 过底面圆的圆心
过底面圆的圆心 ![]() ,
,![]() 是圆
是圆![]() 上不与点
上不与点![]() 、
、![]() 重合的任意一点,已知棱
重合的任意一点,已知棱![]() ,
, ![]() ,
,![]() .
.
(1)求直线![]() 与平面
与平面![]() 所成的角的大小;
所成的角的大小;
(2)将四面体![]() 绕母线
绕母线![]() 转动一周,求
转动一周,求![]() 的三边在旋 转过程中所围成的几何体的体积.
的三边在旋 转过程中所围成的几何体的体积.
查看答案和解析>>
科目:高中数学 来源:2014届广东实验中学高二上学期期中理科数学试卷(解析版) 题型:解答题
(本小题满分12分)
如图,直角梯形ABCD中,∠B=90°,AD//BC,AD=1,BC=2,
∠C=60°,将该梯形绕着AB所在的直线为轴旋转一周,求该旋转体的表面积和体积。

查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市浦东新区高三第三次模拟考试理科数学试卷(解析版) 题型:解答题
(本题满分12分,每一问6分)
如图,弧 是半径为
是半径为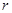 的半圆,
的半圆,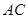 为直径,点
为直径,点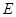 为弧
为弧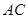 的中点,点
的中点,点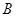 和点
和点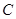 为线段
为线段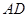 的三等分点,线段
的三等分点,线段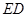 与弧
与弧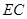 交于点
交于点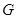 ,且
,且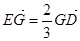 ,平面
,平面 外一点
外一点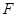 满足
满足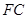
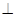 平面
平面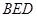 ,
,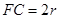 。
。

⑴证明:
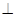
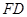 ;
;
⑵ 将 (及其内部)绕
(及其内部)绕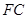 所在直线旋转一周形成一几何体,求该几何体的体积。
所在直线旋转一周形成一几何体,求该几何体的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
如图,△VAC中,![]() ,将其绕直线VC旋转得到△VBC,D是AB的中点,
,将其绕直线VC旋转得到△VBC,D是AB的中点,![]()
(Ⅰ)求证:平面VAB⊥平面VCD;
(Ⅱ)当角θ变化时,求直线BC与平面VAB所成的角的取值范围.
(Ⅲ)当![]() 时,在线段VB上能否找到点E使二面角E—CD—B的大小为
时,在线段VB上能否找到点E使二面角E—CD—B的大小为![]() ,若能,求
,若能,求![]() ;若不能,说明理由。
;若不能,说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com