
 在区间
在区间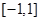 上是增函数,实数a组成几何A,设关于x的方程
上是增函数,实数a组成几何A,设关于x的方程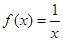 的两个非零实根
的两个非零实根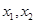 ,实数m使得不等式
,实数m使得不等式 使得对任意
使得对任意 及
及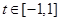 恒成立,则m的解集是( )
恒成立,则m的解集是( )A.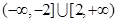 | B.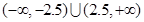 |
C. | D. |
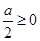 ,φ(-1)=1+a-2≤0或
,φ(-1)=1+a-2≤0或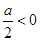 ,φ(1)=1-a-2≤0?0≤a≤1或-1≤a≤0
,φ(1)=1-a-2≤0?0≤a≤1或-1≤a≤0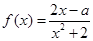 =
=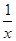 ,得x2-ax-2=0,∵△=a2+8>0,∴x1,x2是方程x2-ax-2=0的两非零实根,x1+x2=a,x1x2=-2,从而|x1-x2|==
,得x2-ax-2=0,∵△=a2+8>0,∴x1,x2是方程x2-ax-2=0的两非零实根,x1+x2=a,x1x2=-2,从而|x1-x2|==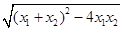 =
=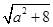 ∵-1≤a≤1,∴|x1-x2|=
∵-1≤a≤1,∴|x1-x2|=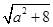 ≤3.
≤3.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
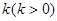 .现已知相距
.现已知相距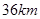 的
的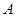 ,
,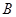 两家化工厂(污染源)的污染强度分别为正数
两家化工厂(污染源)的污染强度分别为正数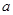 ,
,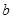 ,它们连线上任意一点C处的污染指数
,它们连线上任意一点C处的污染指数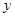 等于两化工厂对该处的污染指数之和.设
等于两化工厂对该处的污染指数之和.设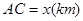 .
.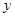 表示为
表示为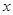 的函数;
的函数; 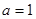 时,
时,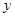 在
在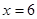 处取得最小值,试求
处取得最小值,试求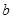 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com