
如图,在四棱锥 中,底面
中,底面 是直角梯形,
是直角梯形, ,
, ,
,
平面 平面
平面 ,若
,若
 ,
, ,
,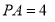 ,
, ,且
,且 .
.

(1)求证: 平面
平面 ;
;
(2)设平面 与平面
与平面 所成二面角的大小为
所成二面角的大小为 ,求
,求 的值.
的值.
(1)参考解析;(2)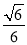
【解析】
试题分析:(1)由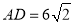 ,
,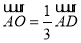 所以
所以 .又
.又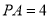 ,
,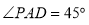 .在三角形PAO中由余弦定理可得
.在三角形PAO中由余弦定理可得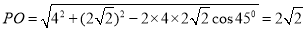 .所以
.所以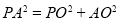 .即
.即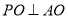 .又平面
.又平面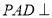 平面
平面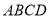 且平面
且平面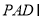 平面
平面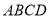 =AD,
=AD,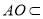 平面PAD.所以
平面PAD.所以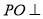 平面
平面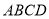 .
.
(2)由题意可得建立空间坐标系,写出相应点的坐标,平面PAD的法向量易得,用待定系数写出平面PBC的法向量,根据两向量的法向量夹角的余弦值,求出二面角的余弦值.
(1)因为  ,
,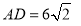 ,所以
,所以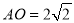 , 1分
, 1分
在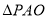 中,由余弦定理
中,由余弦定理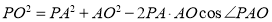 ,
,
得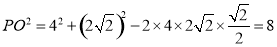 , 3分
, 3分
 ,
,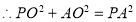 , 4分
, 4分
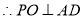 , 5分
, 5分
又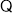 平面
平面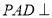 平面
平面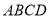 ,平面
,平面 平面
平面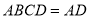 ,
,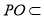 平面
平面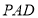 ,
,
 平面
平面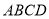 . 6分
. 6分
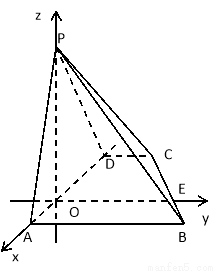
(2)如图,过 作
作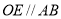 交
交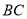 于
于 ,则
,则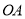 ,
,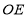 ,
,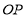 两两垂直,以
两两垂直,以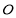 为坐标原点,分别以
为坐标原点,分别以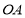 ,
,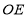 ,
,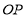 所在直线为
所在直线为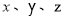 轴,建立空间直角坐标系
轴,建立空间直角坐标系 , 7分
, 7分
则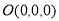 ,
,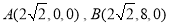 ,
,
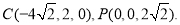 8分
8分
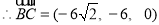 ,
,
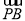
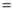
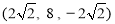 , 9分
, 9分
设平面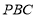 的一个法向量为
的一个法向量为 ,
,
由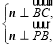
 得
得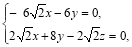 即
即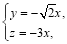
取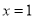 则
则 ,
,
所以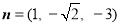 为平面
为平面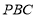 的一个法向
的一个法向
量. 11分
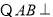 平面
平面 ,
, 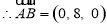 为平面
为平面 的
的
一个法向量.
所以 
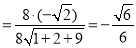 , 12分
, 12分
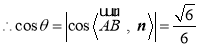 . 13分
. 13分
考点:1.线面垂直的证明.2.二面角.3.空间坐标系的表示.4.向量的夹角.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源:2013-2014学年福建省高考考前模拟文科数学试卷(解析版) 题型:选择题
已知曲线 :
: 和
和 :
: 的焦点分别为
的焦点分别为 、
、 ,点
,点 是
是 和
和 的一个交点,则△
的一个交点,则△ 的形状是( )
的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.都有可能
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省厦门市高三5月适应性考试理科数学试卷(解析版) 题型:选择题
数列 的前
的前 项和为
项和为 ,前
,前 项积为
项积为 ,且
,且 ,则
,则 等于( )
等于( )
 A.31 B.62 C.124 D.126
A.31 B.62 C.124 D.126
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省三明市高三5月质量检查理科数学试卷(解析版) 题型:解答题
已知在平面直角坐标系 中,圆
中,圆 的方程为
的方程为 .以原点
.以原点 为极点,以
为极点,以 轴正半轴为极轴,且与直角坐标系取相同的单位长度,建立极坐标系,直线
轴正半轴为极轴,且与直角坐标系取相同的单位长度,建立极坐标系,直线 的极坐标方程为
的极坐标方程为 .
.
(1)求直线 的直角坐标方程和圆
的直角坐标方程和圆 的参数方程;
的参数方程;
(2)求圆 上的点到直线
上的点到直线 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省三明市高三5月质量检查理科数学试卷(解析版) 题型:选择题
在二项式 的展开式中恰好第5项的二项式系数最大,则展开式中含
的展开式中恰好第5项的二项式系数最大,则展开式中含 项的系数是( )
项的系数是( )
A.-56 B.-35 C.35 D.56
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省三明市高三5月质量检查文科数学试卷(解析版) 题型:选择题
对于函数 在定义域内的任意实数
在定义域内的任意实数 及
及 ,都有
,都有 及
及
 成立,则称函数
成立,则称函数 为“
为“ 函数”.现给出下列四个函数:
函数”.现给出下列四个函数:


 ;
; .其中是“
.其中是“ 函数”的是( )
函数”的是( )
A. B.
B. C.
C.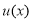 D.
D.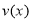
查看答案和解析>>
科目:高中数学 来源:2013-2014学年甘肃省武威市高三数学专题训练选择填空限时练五(解析版) 题型:填空题
在△ABC中,角A,B,C所对的边分别为a,b,c,已知a=2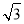 ,c= 2
,c= 2 ,1+
,1+ =
= ,则C=________.
,则C=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com