
分析 令g(x)=$\frac{f(x)}{x}$,根据函数的单调性和函数的奇偶性求出不等式的解集即可.
解答 解:令g(x)=$\frac{f(x)}{x}$,
∵x>0时,g′(x)=$\frac{xf′(x)-f(x)}{{x}^{2}}$<0,
∴g(x)在(0,+∞)递减,
∵f(-x)=f(x),
∴g(-x)=$\frac{f(-x)}{-x}$=-g(x),
g(x)在(-∞,0)递减,
∴g(x)是奇函数,
g(2)=$\frac{f(2)}{2}$=0,
∴0<x<2时,g(x)>0,x>2时,g(x)<0,
根据函数的奇偶性,-2<x<0时,g(x)<0,x<-2时,g(x)>0,
xf(x)<0,即x2g(x)<0,即g(x)<0,
∴x>2或-2<x<0,
故答案为:(-2,0)∪(2,+∞).
点评 本题主要考察函数奇偶性的应用,考查函数的单调性,是一道中档题.


 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:选择题
| A. | (-3,1) | B. | $(-1+\sqrt{3},1)∪(-3,-1-\sqrt{3})$ | C. | $(-1-\sqrt{3},-1+\sqrt{3})$ | D. | $(-∞,-1-\sqrt{3})∪(-1+\sqrt{3},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
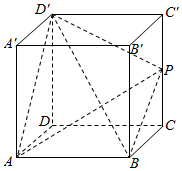 在棱长为4的正方体ABCD-A′B′C′D′中,点P在棱CC′上,且CC′=2CP.
在棱长为4的正方体ABCD-A′B′C′D′中,点P在棱CC′上,且CC′=2CP.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知在多面体SP-ABCD中,底面ABCD为矩形,AB=PC=1,AD=AS=2,且AS∥CP且AS⊥面ABCD,E为BC的中点.
已知在多面体SP-ABCD中,底面ABCD为矩形,AB=PC=1,AD=AS=2,且AS∥CP且AS⊥面ABCD,E为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
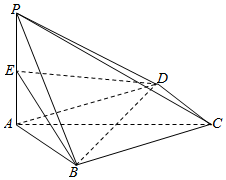 如图,四棱锥P-ABCD中,ABCD是边长为2的菱形,且∠DAB=60°,PC=4,PA=2,E是PA的中点,平面PAC⊥平面ABCD.
如图,四棱锥P-ABCD中,ABCD是边长为2的菱形,且∠DAB=60°,PC=4,PA=2,E是PA的中点,平面PAC⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{3}$) | B. | (-∞,0] | C. | (-∞,1) | D. | (-$\frac{1}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com