
【题目】如图,在四棱锥P-ABCD中,E是PC的中点,底面ABCD为矩形,AB=4,AD=2,PA=PD,且平面PAD⊥平面ABCD,平面ABE与棱PD交于点F.

(1)求证:EF∥平面PAB;
(2)若PB与平面ABCD所成角的正弦值为![]() ,求二面角P-AE-B的余弦值.
,求二面角P-AE-B的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)利用AB∥平面PCD,可得AB∥EF,即可证明;(2)取AD中点O,连结OP,以O为原点,OA为x轴,在平面ABCD中,过O作AB的平行线为y轴,以OP为z轴,建立空间直角坐标系,利用向量法能求出二面角P-AE-B的余弦值.
(1)矩形ABCD中,AB∥CD,
∵AB面PCD,CD平面PCD,
∴AB∥平面PCD,
又AB平面ABE,
平面PCD∩平面ABE=EF,
∴AB∥EF,
∵EF面PAB,AB平面PAB,
∴EF∥平面PAB.
(2)取AD中点O,连结OP,
∵在四棱锥P-ABCD中,底面ABCD为矩形,AB=4,AD=2,PA=PD,且平面PAD⊥平面ABCD,
∴PO⊥底面ABCD,连接OB,则OB为PB在平面ABCD内的射影,
∴∠PBO为PB与平面ABCD所成角,根据题意知sin∠PBO=![]() ,
,
∴tan∠PBO=![]() ,由题OB=
,由题OB=![]() ,∴PO=2
,∴PO=2
取BC中点G,连接OG,以O为坐标原点,OA为x轴,在平面ABCD中,过O作AB的平行线为y轴,以OP为z轴,建立空间直角坐标系,
B(1,4,0),设P(0,0,2),C=(-1,4,0),E(-![]() ,2,1)
,2,1)

![]() ,
,![]()
设平面PAE的法向量为![]() ,
,
于是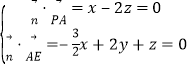 ,
,
令x=2,则y=1,z=1
∴平面PAE的一个法向量![]() =(2,1,1),
=(2,1,1),
同理平面ABE的一个法向量为![]() =(2,0,3),
=(2,0,3),
∴cos![]() =
=![]()
可知二面角P-AE-B为钝二面角
所以二面角P-AE-B的余弦值为-![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】大连市某企业为确定下一年投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年销售量
(单位:千元)对年销售量![]() (单位:
(单位:![]() )和年利润
)和年利润![]() (单位:千元)的影响,对近8年的年宣传费
(单位:千元)的影响,对近8年的年宣传费![]() 和年销售量
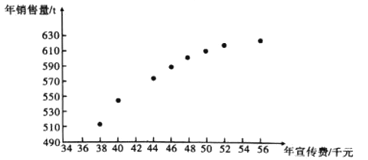
和年销售量![]() 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
46.6 | 573 | 6.8 | 289.8 | 1.6 | 215083.4 | 31280 |
表中![]() ,
,![]() .
.
![]() 根据散点图判断,
根据散点图判断,![]() 与
与![]() 哪一个适宜作为年销售量
哪一个适宜作为年销售量![]() 关于年宣传费
关于年宣传费![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
![]() 根据
根据![]() 的判断结果及表中数据,建立
的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
![]() 已知这种产品的年利润
已知这种产品的年利润![]() 与
与![]() 、
、![]() 的关系为
的关系为![]() .根据
.根据![]() 的结果回答下列问题:
的结果回答下列问题:
![]() 年宣传费
年宣传费![]() 时,年销售量及年利润的预报值是多少?
时,年销售量及年利润的预报值是多少?
![]() 年宣传费
年宣传费![]() 为何值时,年利润的预报值最大?
为何值时,年利润的预报值最大?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
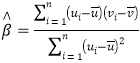 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() =1(a>0,b>0)的右焦点为F,P,Q为双曲线上关于原点对称的两点,若
=1(a>0,b>0)的右焦点为F,P,Q为双曲线上关于原点对称的两点,若![]() =0,且∠POF<
=0,且∠POF<![]() ,则该双曲线的离心率的取值范围为______.
,则该双曲线的离心率的取值范围为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() =1(a>b>0)的右焦点为F(2,0),且过点(2
=1(a>b>0)的右焦点为F(2,0),且过点(2![]() ,
,![]() ).
).
(1)求椭圆的标准方程;
(2)设直线l:y=kx(k>0)与椭圆在第一象限的交点为M,过点F且斜率为-1的直线与l交于点N,若![]() sin∠FON(O为坐标原点),求k的值.
sin∠FON(O为坐标原点),求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:方程x2+(2m-4)x+m=0有两个不等的实数根:命题q:x∈[2,3],不等式x2-4x+13≥m2恒成立.
(1)若命题p为真命题,则实数m的取值范围;
(2)若命题p∨q为真命题,命题p∧q为假命题,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,平面
,平面![]() 底面
底面![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 是棱
是棱![]() 上的点,
上的点,![]() ,
,![]() ,
,![]() .
.
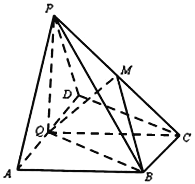
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 为棱
为棱![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(3)若二面角![]() 大小为
大小为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}中,a1=8,a4=2,且满足an+2-2an+1+an=0.
(1)求数列的通项公式;
(2)设Sn=|a1|+|a2|+…+|an|,求Sn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com