
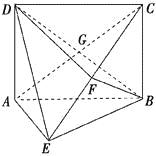
【题目】如图所示,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.
(1)求证:AE⊥平面BCE;
(2)求证:AE∥平面BFD;
(3)求三棱锥C-BGF的体积.
【答案】(1)见详解;(2)见详解;(3)![]()
【解析】
(1)证明 ∵AD⊥平面ABE,AD∥BC, ∴BC⊥平面ABE,则AE⊥BC.
又∵BF⊥平面ACE,则AE⊥BF,
又BC∩BF=B,∴AE⊥平面BCE.
(2)证明 由题意可得G是AC的中点,连结FG,
∵BF⊥平面ACE,∴CE⊥BF.
而BC=BE,∴F是EC的中点,
在△AEC中,FG∥AE,∴AE∥平面BFD.
(3)∵AE∥FG.
而AE⊥平面BCE,
∴FG⊥平面BCF.
∵G是AC中点,F是CE中点,
∴FG∥AE且FG=![]() AE=1.
AE=1.
∴Rt△BCE中,BF=CE=CF=![]() ,
,
∴S△CFB=![]() ×
×![]() ×
×![]() =1.
=1.
∴VC-BGF=VG-BCF=·S△CFB·FG=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】若![]() 、
、![]() 、
、![]() 均为正整数,且
均为正整数,且![]() ,
,![]() 为一素数,
为一素数,![]() 、
、![]() 、
、![]() 的
的![]() 进制表示分别为
进制表示分别为![]() ,其中,
,其中,![]() .证明:
.证明:
(1)若![]() ,且对整数
,且对整数![]()
![]() 均有
均有![]() ,则
,则![]() ,其中,
,其中,![]() 表示不超过实数
表示不超过实数![]() 的最大整数.
的最大整数.
(2)![]()
![]() ,其中,
,其中,![]() 表示集合A中元素的个数.
表示集合A中元素的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名射击运动员一次射击命中目标的概率分别是0.7,0.6,且每次射击命中与否相互之间没有影响,求:
(1)甲射击三次,第三次才命中目标的概率;
(2)甲、乙两人在第一次射击中至少有一人命中目标的概率;
(3)甲、乙各射击两次,甲比乙命中目标的次数恰好多一次的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国足球甲![]() 联赛共有12个足球俱乐部参加,实行主客场双循环赛制,即任何两队分别在主场和客场各比赛一场,胜一场得3分,平一场各得1分,负一场得0分,在联赛结束后按积分的高低排出名次.则在积分榜上位次相邻的两支球队积分差距最多可达_________分.
联赛共有12个足球俱乐部参加,实行主客场双循环赛制,即任何两队分别在主场和客场各比赛一场,胜一场得3分,平一场各得1分,负一场得0分,在联赛结束后按积分的高低排出名次.则在积分榜上位次相邻的两支球队积分差距最多可达_________分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 命题![]() ,
,![]() 都是假命题,则命题“
都是假命题,则命题“![]() ”为真命题.
”为真命题.
B. ![]() ,函数
,函数![]() 都不是奇函数.
都不是奇函数.
C. 函数![]() 的图像关于
的图像关于![]() 对称 .
对称 .
D. 将函数![]() 的图像上所有点的横坐标伸长到原来的2倍后得到
的图像上所有点的横坐标伸长到原来的2倍后得到![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若![]() 为偶函数,求
为偶函数,求![]() 的值并写出
的值并写出![]() 的增区间;
的增区间;
(Ⅱ)若关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,当
,当![]() 时,求
时,求![]() 的最小值;
的最小值;
(Ⅲ)对任意的![]() ,
,![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
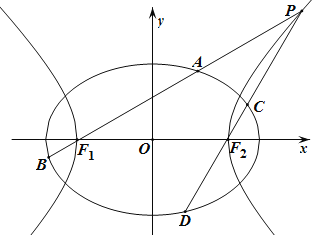
如图,已知椭圆![]() 的离心率为
的离心率为![]() ,以该椭圆上的点和椭圆的左、右焦点
,以该椭圆上的点和椭圆的左、右焦点![]() 为顶点的三角形的周长为
为顶点的三角形的周长为![]() .一等轴双曲线的顶点是该椭圆的焦点,设
.一等轴双曲线的顶点是该椭圆的焦点,设![]() 为该双曲线上异于顶点的任一点,直线
为该双曲线上异于顶点的任一点,直线![]() 和
和![]() 与椭圆的交点分别为
与椭圆的交点分别为![]() 和
和![]() .
.
(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,证明
,证明![]() ;
;
(Ⅲ)是否存在常数![]() ,使得
,使得![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过坐标原点的直线l与圆C:x2+y2﹣8x+12=0相交于不同的两点A,B.
(1)求线段AB的中点P的轨迹M的方程.
(2)是否存在实数k,使得直线l1:y=k(x﹣5)与曲线M有且仅有一个交点?若存在,求出k的取值范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com