
 )是函数f(x)=ax(a>0),且a≠1的图象上一点,
)是函数f(x)=ax(a>0),且a≠1的图象上一点, +
+ (n≥2).
(n≥2). }前n项和为Tn,问Tn>
}前n项和为Tn,问Tn> 的最小正整数n是多少?
的最小正整数n是多少?解:(1)由已知f(1)=a= ,∴f(x)=
,∴f(x)=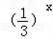 ,
,
等比数列{an}的前n项和为f(n)﹣c=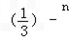 c,
c,
∴a1=f(1)= ﹣c,a2=[f(2)﹣c]﹣[f(1)﹣c]=﹣
﹣c,a2=[f(2)﹣c]﹣[f(1)﹣c]=﹣ ,a3=[f(3)﹣c]﹣[f(2)﹣c]=﹣
,a3=[f(3)﹣c]﹣[f(2)﹣c]=﹣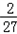
数列{an}是等比数列,应有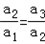 =q,解得c=1,q=
=q,解得c=1,q= .
.
∴首项a1=f(1)= ﹣c=
﹣c=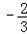
∴等比数列{an}的通项公式为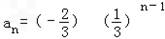 =
=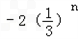 .
.
∵Sn﹣Sn﹣1=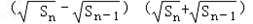 =
=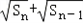 (n≥2)
(n≥2)
又bn>0,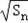 >0,∴
>0,∴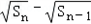 =1;
=1;
∴数列{ 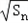 }构成一个首项为1,公差为1的等差数列,∴
}构成一个首项为1,公差为1的等差数列,∴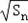 =1+(n﹣1)×1=n
=1+(n﹣1)×1=n
∴Sn=n2 当n=1时,b1=S1=1,
当n≥2时,bn=Sn﹣Sn﹣1=n2﹣(n﹣1)2=2n﹣1
又n=1时也适合上式,∴{bn}的通项公式bn=2n﹣1.
(2)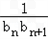 =
=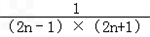 =
=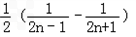
∴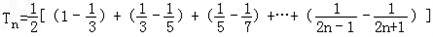 =
=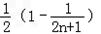 =
=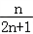
由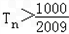 ,得
,得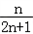
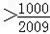 ,
,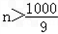 ,
,
故满足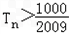 的最小正整数为112.
的最小正整数为112.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
| 1 |
| 3 |
| Sn |
| Sn-1 |
| 1 |
| bnbn+1 |
| 1000 |
| 2011 |
| 2bn |
| a n |
查看答案和解析>>
科目:高中数学 来源:2015届辽宁实验中学分校高二上学期期中考试文科数学试卷(解析版) 题型:解答题
已知点(1, )是函数
)是函数 且
且 )的图象上一点,等比数列
)的图象上一点,等比数列 的前
的前 项和为
项和为 ,数列
,数列
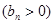 的首项为
的首项为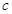 ,且前
,且前 项和
项和 满足
满足 -
- =
= +
+ (
( ).
).
(1)求数列 和
和 的通项公式;
的通项公式;
(2)求数列{ 前
前 项和为
项和为 .
.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省深圳市南头中学高二(上)第一次考试数学试卷(解析版) 题型:解答题
 )是函数f(x)=ax(a>0),且a≠1)的图象上一点,等比数列{an}的前n项和为f(n)-c,数列{bn}(bn>0)的首项为c,且前n项和Sn满足Sn-Sn-1=
)是函数f(x)=ax(a>0),且a≠1)的图象上一点,等比数列{an}的前n项和为f(n)-c,数列{bn}(bn>0)的首项为c,且前n项和Sn满足Sn-Sn-1= +
+ (n≥2).
(n≥2). }前n项和为Tn,问Tn>
}前n项和为Tn,问Tn> 的最小正整数n是多少?
的最小正整数n是多少?查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建师大附中高三(上)期中数学试卷(文科)(解析版) 题型:解答题
 )是函数f(x)=ax(a>0),且a≠1)的图象上一点,等比数列{an}的前n项和为f(n)-c,数列{bn}(bn>0)的首项为c,且前n项和Sn满足Sn-Sn-1=
)是函数f(x)=ax(a>0),且a≠1)的图象上一点,等比数列{an}的前n项和为f(n)-c,数列{bn}(bn>0)的首项为c,且前n项和Sn满足Sn-Sn-1= +
+ (n≥2).
(n≥2). }前n项和为Tn,问Tn>
}前n项和为Tn,问Tn> 的最小正整数n是多少?
的最小正整数n是多少?查看答案和解析>>
科目:高中数学 来源:2013届河南省商丘市高二第一学期第二次月考数学试卷 题型:解答题
(本题满分12分) 已知点(1, )是函数
)是函数 且
且 )的图象上一点,等比数列
)的图象上一点,等比数列 的前
的前 项和为
项和为 ,数列
,数列
 的首项为
的首项为 ,且前
,且前 项和
项和 满足
满足 -
- =
= +
+ (
(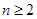 ).
).
(1)求数列 和
和 的通项公式;
的通项公式;
(2)若数列{ 前
前 项和为
项和为 ,问
,问 >
> 的最小正整数
的最小正整数 是多少?
是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com