解:(I)由sin(x+a)=sin(-x)得sin(x+a)=-sinx,
根据诱导公式得a=2kπ+π(k∈Z).
∴y=sinx具有“P(a)性质”,其中a=2kπ+π(k∈Z).…(4分)
(II)∵y=g(x)具有“P(±1)性质”,
∴g(1+x)=g(-x),g(-1+x)=g(-x),
∴g(x+2)=g(1+1+x)=g(-1-x)=g(x),从而得到y=g(x)是以2为周期的函数.
又设

≤x≤

,则-

≤1-x≤

,
g(x)=g(x-2)=g(-1+x-1)=g(-x+1)=|-x+1|=|x-1|=g(x-1).
再设n-

≤x≤n+

(n∈z),
当n=2k(k∈z),2k-

≤x≤2k+

,则-

≤x-2k≤

,
g(x)=g(x-2k)=|x-2k|=|x-n|;
当n=2k+1(k∈z),2k+1-

≤x≤2k+1+

,则

≤x-2k≤

,
g(x)=g(x-2k)=|x-2k-1|=|x-n|;
∴对于,n-

≤x≤n+

(n∈z),都有g(x)=|x-n|,而n+1-

≤x+1≤n+1+

,
∴g(x+1)=|(x+1)-(n+1)|=|x-n|=g(x),
∴y=g(x)是周期为1的函数.
①当m>0时,要使y=mx与y=g(x)有2013个交点,只要y=mx与y=g(x)在[0,1006)有2012个交点,而在[1006,1007]有一个交点.
∴y=mx过(
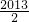
,

),从而得m=

②当m<0时,同理可得m=-

③当m=0时,不合题意.
综上所述m=±

…(14分)
分析:(I)根据题意先检验sin(x+a)=sin(-x)是否成立即可检验y=sinx是否具有“P(a)性质”
(II)由题意可得g(1+x)=g(-x),g(-1+x)=g(-x),据此递推关系可推断函数y=g(x)的周期,根据交点周期性出现的规律即可求解满足条件的m.
点评:本题考查周期函数,着重考查函数在一定条件下的恒成立问题,综合考察构造函数、分析转化、分类讨论的数学思想与方法,难度大,思维深刻,属于难题.

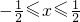 时,g(x)=|x|.若y=g(x)与y=mx交点个数为2013个,求m的值.
时,g(x)=|x|.若y=g(x)与y=mx交点个数为2013个,求m的值. ≤x≤
≤x≤ ,则-
,则- ≤1-x≤
≤1-x≤ ,
, ≤x≤n+
≤x≤n+ (n∈z),
(n∈z), ≤x≤2k+
≤x≤2k+ ,则-
,则- ≤x-2k≤
≤x-2k≤ ,
, ≤x≤2k+1+
≤x≤2k+1+ ,则
,则 ≤x-2k≤
≤x-2k≤ ,
, ≤x≤n+
≤x≤n+ (n∈z),都有g(x)=|x-n|,而n+1-
(n∈z),都有g(x)=|x-n|,而n+1- ≤x+1≤n+1+
≤x+1≤n+1+ ,
,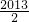 ,
, ),从而得m=
),从而得m=

 …(14分)
…(14分)
