
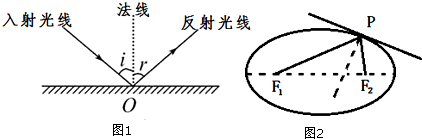
分析 (1)因为桌球第一次与球桌边缘的接触点可能椭圆长轴的两个端点及这两个端点外的任一点三种情况,分别表示出S=2(a-c)或S=2(a+c)或S=4a;
(2)求得M点坐标,求得直线MA和MB的方程,将M点坐标代入,即可求得直线AB方程$\frac{\sqrt{3}}{3}$x+ty-1,直线AB恒过定点$F({\sqrt{3},0})$;求得椭圆的切线方程,由直线PI⊥l,${l_{PI}}:y=\frac{{4{y_0}}}{x_0}x-3{y_0}$,y=0,得点N的横坐标为${x_N}=\frac{{3{x_0}}}{4}$,根据x0的取值范围,即可求得点N横坐标的取值范围.
解答 解:(1)记$c=\sqrt{{a^2}-{b^2}}$,
因为桌球第一次与球桌边缘的接触点可能椭圆长轴的两个端点及这两个端点外的任一点三种情况,
所以S=2(a-c)或S=2(a+c)或S=4a;[(4分)]
(2)①设$M({\frac{{4\sqrt{3}}}{3},t})({t∈R}),A({{x_1},{y_1}}),B({{x_2},{y_2}})$,则…[(5分)],
${l_{MA}}:\frac{{{x_1}x}}{4}+{y_1}y=1,{l_{MB}}:\frac{{{x_2}x}}{4}+{y_2}y=1$,…[(6分)]
代入$M({\frac{{4\sqrt{3}}}{3},t})$,得${l_{MA}}:\frac{{\sqrt{3}}}{3}{x_1}+t{y_1}=1,{l_{MB}}:\frac{{\sqrt{3}}}{3}{x_2}+t{y_2}=1$,…[(7分)]
则点A,B的坐标均满足方程$\frac{{\sqrt{3}}}{3}x+ty=1,即{l_{AB}}:\frac{{\sqrt{3}}}{3}x+ty-1=0$,…[(9分)]
所以,直线AB恒过定点$F({\sqrt{3},0})$;…[(10分)]
②由(2)的结论知:椭圆C在P(x0,y0)处的切线l的方程为$\frac{{{x_0}x}}{4}+{y_0}y=1$,…[(11分)]
由事实现象(2)知:直线PI⊥l,
∴${l_{PI}}:y=\frac{{4{y_0}}}{x_0}x-3{y_0}$…[(13分)]
令y=0,得点N的横坐标为${x_N}=\frac{{3{x_0}}}{4}$,…[(15分)]
∵x0∈(0,2),
∴${x_N}∈({0,\frac{3}{2}})$.…[(16分)]
点评 本题考查椭圆方程的实际应用,考查直线与椭圆的位置关系,直线的切线方程,考查计算能力,属于中档题.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | l与m,n都相交 | B. | l与m,n中至少一条相交 | ||
| C. | l与m,n都不相交 | D. | l只与m,n中一条相交 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
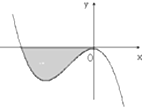 已知函数f(x)=-x3+ax2+bx(a,b∈R)的图象如图所示,它与x轴在原点相切,且x轴与函数图象所围成的区域(如图阴影部分)的面积为$\frac{1}{12}$,则a的值为-1.
已知函数f(x)=-x3+ax2+bx(a,b∈R)的图象如图所示,它与x轴在原点相切,且x轴与函数图象所围成的区域(如图阴影部分)的面积为$\frac{1}{12}$,则a的值为-1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com