
已知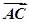 =(cos
=(cos +sin
+sin ,-sin
,-sin ),
),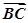 =(cos
=(cos -sin
-sin ,2cos
,2cos ).
).
(1)设f(x)=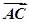 ·
·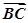 ,求f(x)的最小正周期和单调递减区间;
,求f(x)的最小正周期和单调递减区间;
(2)设有不相等的两个实数x1,x2∈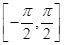 ,且f(x1)=f(x2)=1,求x1+x2的值.
,且f(x1)=f(x2)=1,求x1+x2的值.
(1) T=2π
f(x)的单调递减区间是[- +2kπ,
+2kπ,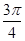 +2kπ](k∈Z)
+2kπ](k∈Z)
(2) x1+x2=-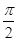
【解析】本试题主要是考查了向量的数量积公式以及三角函数的图像与性质的综合运用。注意解三角方程,要看范围。
解:(1)由f(x)=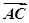 ·
·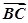 得
得
f(x)=(cos +sin
+sin )·(cos
)·(cos -sin
-sin )+(-sin
)+(-sin )·2cos
)·2cos
=cos2 -sin2
-sin2 -2sin
-2sin cos
cos =cosx-sinx=
=cosx-sinx= cos(x+
cos(x+ ),...........4分
),...........4分
所以f(x)的最小正周期T=2π.............6分
又由2kπ≤x+ ≤π+2kπ,k∈Z,
≤π+2kπ,k∈Z,
得- +2kπ≤x≤
+2kπ≤x≤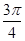 +2kπ,k∈Z.
+2kπ,k∈Z.
故f(x)的单调递减区间是[- +2kπ,
+2kπ,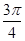 +2kπ](k∈Z) ……..8分
+2kπ](k∈Z) ……..8分
(2)由f(x)=1得 cos(x+
cos(x+ )=1,故cos(x+
)=1,故cos(x+ )=
)=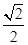 ……10分
……10分
又x∈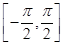 ,于是有x+
,于是有x+ ∈
∈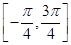 ,得x1=0,x2=-
,得x1=0,x2=-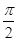 ,
,
所以x1+x2=-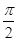


科目:高中数学 来源:聊城一中高三数学测试——平面向量 题型:044
已知![]() =(cosα,sinα),
=(cosα,sinα),![]() =(cosβ,sinβ),且
=(cosβ,sinβ),且![]() 与
与![]() 之间满足关系:
之间满足关系:![]() ,其中k>0.
,其中k>0.
(Ⅰ)用k表示![]() ·
·![]() ;
;
(Ⅱ)求![]() ·
·![]() 的最小值,并求此时
的最小值,并求此时![]() 与
与![]() 夹角
夹角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)已知![]() =(cos+sin,-sin),
=(cos+sin,-sin),![]() =(cos-sin,2cos).
=(cos-sin,2cos).
(1)设f(x)=![]() ·
·![]() ,求f(x)的最小正周期和单调递减区间;
,求f(x)的最小正周期和单调递减区间;
(2)设有不相等的两个实数x1,x2∈,且f(x1)=f(x2)=1,求x1+x2的值.
查看答案和解析>>
科目:高中数学 来源:2014届河北衡水中学高一第二学期期末文科数学试卷(解析版) 题型:解答题
(本小题满分12分)
已知 =(cos
=(cos +sin
+sin ,-sin
,-sin ),
), =(cos
=(cos -sin
-sin ,2cos
,2cos ).
).
(1)设f(x)= ·
· ,求f(x)的最小正周期和单调递减区间;
,求f(x)的最小正周期和单调递减区间;
(2)设有不相等的两个实数x1,x2∈ ,且f(x1)=f(x2)=1,求x1+x2的值.
,且f(x1)=f(x2)=1,求x1+x2的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com