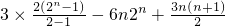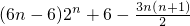Question

数列{a_n}的前n项和为S_n，若对于任意的正整数n都有S_n=2a_n-3n．
（1）设b_n=a_n+3，求证：数列{b_n}是等比数列，并求出{a_n}的通项公式；
（2）求数列{na_n}的前n项和．

Answer 1

解：（1）∵S_n=2a_n-3n，对于任意的正整数都成立，
∴S_n+1=2a_n+1-3n-3，
两式相减，得a _n+1=2a_n+1-2a_n-3，即a_n+1=2a_n+3，
∴a_n+1+3=2（a_n+3），
所以数列{b_n}是以2为公比的等比数列，
由已知条件得：S₁=2a₁-3，a₁=3．
∴首项b₁=a₁+3=6，公比q=2，
∴a_n=6•2^n-1-3=3•2ⁿ-3．
（2）∵na_n=3×n•2ⁿ-3n
∴S_n=3（1•2+2•2²+3•2³+…+n•2ⁿ）-3（1+2+3+…+n），
2S_n=3（1•2²+2•2³+3•2⁴+…+n•2ⁿ⁺¹）-6（1+2+3+…+n），
∴-S_n=3（2+2²+2³+…+2ⁿ-n•2ⁿ⁺¹）+3（1+2+3+…+n）
=
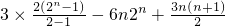
∴S_n=
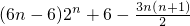
分析：（1）通过递推关系式求出a_n与a_n+1的关系，推出{a_n+3}即数列{b_n}是等比数列，求出数列{b_n}的通项公式即可求出{a_n}的通项公式；
（2）写出数列{na_n}的通项公式，然后写出前n项和的表达式通过错位相减法求解即可．
点评：本题考查数列递推式，等比关系的确定，数列的求和的方法---错位相减法的应用，高考参考题型，考查计算能力．