
分析 (1)利用有理指数幂的运算法则化简求解即可.
(2)利用导数的运算法则化简求解即可.
(3)利用指数式与对数式互化,利用换底公式化简求解即可.
解答 (本题满分12分)
解:(1)原式=${({3^3})^{-\frac{2}{3}}}-1+4$=3-2-1+4=$\frac{1}{9}+3$=$\frac{28}{9}$…(4分)
(2)原式=lg22+lg5(1+lg2)+2
=lg22+lg5lg2+lg5+2
=lg2(lg2+lg5)+lg5+2
=lg2+lg5+2
=3…(8分)
(3)a=log53,b=log54
${log_{25}}12=\frac{{{{log}_5}12}}{{{{log}_5}25}}=\frac{{{{log}_5}3+{{log}_5}4}}{2}=\frac{a+b}{2}$…(12分)
点评 本题考查指数的运算法则以及对数的运算法则的应用,考查计算能力,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{4}或\frac{5}{4}$ | D. | $\frac{3}{4}或\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
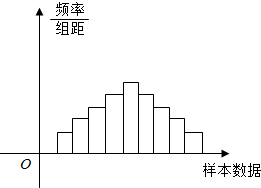 在样本的频率分布直方图中,共有9个小长方形,若第一个长方形的面积为0.04,前五个与后五个长方形的面积分别成等差数列且公差是互为相反数,若样本容量为800,则中间一组(即第五组)的频数为160.
在样本的频率分布直方图中,共有9个小长方形,若第一个长方形的面积为0.04,前五个与后五个长方形的面积分别成等差数列且公差是互为相反数,若样本容量为800,则中间一组(即第五组)的频数为160.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com