下列三个结论中
①命题p:“对于任意的x∈R,都有x2≥0”,则¬p为“存在x∈R,使得x2<0”;②某人5 次上班途中所花的时间(单位:分钟)分别为8、10、11、9、x.已知这组数据的平均数为10,则其方差为2;③若函数f(x)=x2+2ax+2在区间(-∞,4]上是减函数,则实数a的取值范围是(-∞,-4).你认为正确的结论序号为 .
【答案】
分析:①中的命题是一个全称命题,其否定是特称命题,依据全称命题的否定书写形式写出命题的否定即可
②先根据平均数的定义确定出x的值,再根据方差的计算公式S
2=
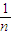
[(x
1-
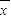
)
2+(x
2-
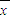
)
2+…+(x
n-
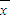
)
2]求出这组数据的方差.
③根据二次函数的单调性与开口方向和对称轴有关,先求出函数的对称轴,然后结合开口方向可知(-∞,4]是(-∞,-a]的子集即可.
解答:解:①∵命题p:对于任意的x∈R,都有x
2≥0,
∴命题p的否定是“存在x∈R,使得x
2<0”正确;
②:由平均数的公式得:(8+10+11+9+x)÷5=10,解得x=12;
∴方差=[(8-10)
2+(10-10)
2+(11-10)
2+(9-10)
2+(12-10)
2]÷5=2.正确;
③:二次函数y=x
2+2ax+2是开口向上的二次函数
对称轴为x=-a,
∴二次函数y=y=x
2+2ax+2在(-∞,-a]上是减函数
∵函数y=x
2+2ax+2在区间(-∞,4]上是减函数,
∴-a≥4,解得a≤-4,错.
故答案为:①②.
点评:本题主要考查全称命题与特称命题的相互转化问题、考查了平均数和方差的定义、二次函数的单调性,二次函数是高考中的热点问题,属于基础题.

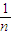 [(x1-
[(x1-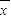 )2+(x2-
)2+(x2-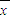 )2+…+(xn-
)2+…+(xn-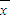 )2]求出这组数据的方差.
)2]求出这组数据的方差.
