
【题目】已知函数![]() .
.
(1)解不等式![]() ;
;
(2)若函数![]() 在区间
在区间![]() 上存在零点,求实数
上存在零点,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() ,其中
,其中![]() 为奇函数,
为奇函数, ![]() 为偶函数,若不等式
为偶函数,若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)(1,3)(2)![]() (3)
(3)![]()
【解析】试题分析:
(1)利用换元法并通过解二次不等式可得2<2x<8,可得1<x<3,即为所求.(2)分离参数可得![]() 在
在![]() 有解,设
有解,设![]() ,求出函数
,求出函数![]() 在区间
在区间![]() 上的值域即为所求范围.(3)根据题意求得
上的值域即为所求范围.(3)根据题意求得![]() 的解析式,然后通过分离参数
的解析式,然后通过分离参数![]() ,将恒成立问题转化为具体函数的最值问题,求解即可.
,将恒成立问题转化为具体函数的最值问题,求解即可.
试题解析:
(1)原不等式即为![]() ,
,
设t=2x,则不等式化为t﹣t2>16﹣9t,
即t2﹣10t+16<0,解得2<t<8,
即2<2x<8,
∴1<x<3
∴原不等式的解集为(1,3).
(2)函数![]() 在
在![]() 上有零点,
上有零点,
所以![]() 在
在![]() 上有解,
上有解,
即![]() 在
在![]() 有解.
有解.
设![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
∴![]() .
.
∵![]() 在
在![]() 有解
有解
∴![]()
故实数m的取值范围为![]() .
.
(3)由题意得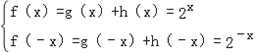 ,
,
解得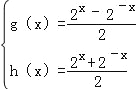 .
.
由题意得![]() ,即
,即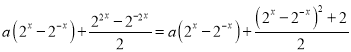
![]() 对任意
对任意![]() 恒成立,
恒成立,
令![]() ,则
,则![]() .
.
则得![]() 对任意的
对任意的![]() 恒成立,
恒成立,
∴![]() 对任意的
对任意的![]() 恒成立,
恒成立,
因为![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() .
.
所以![]() .
.
∴实数![]() 的取值范围
的取值范围![]() .
.


科目:高中数学 来源: 题型:
【题目】下列说法: ①分类变量A与B的随机变量K2越大,说明“A与B有关系”的可信度越大.
②以模型y=cekx去拟合一组数据时,为了求出回归方程,设z=lny,将其变换后得到线性方程z=0.3x+4,则c,k的值分别是e4和0.3.
③根据具有线性相关关系的两个变量的统计数据所得的回归直线方程为y=a+bx中,b=1, ![]() =1,
=1, ![]() =3,
=3,
则a=1.正确的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,记
,记![]()
![]() .
.
(Ⅰ)求![]() 的单调递减区间;
的单调递减区间;
(Ⅱ)若![]() ,求
,求 ![]() 的值;
的值;
(Ⅲ)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位得到
个单位得到![]() 的图象,若函数
的图象,若函数![]() 在
在![]() 上有零点,求实数
上有零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R的函数![]() 是偶函数,且满足
是偶函数,且满足![]() 上的解析式为
上的解析式为![]() ,过点
,过点![]() 作斜率为k的直线l,若直线l与函数
作斜率为k的直线l,若直线l与函数![]() 的图象至少有4个公共点,则实数k的取值范围是
的图象至少有4个公共点,则实数k的取值范围是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥 ![]() 的底面为直角梯形,
的底面为直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 底面
底面 ![]() ,
, ![]() 为
为 ![]() 的中点.
的中点.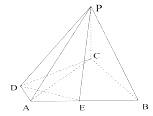
(Ⅰ)求证:平面 ![]() 平面
平面 ![]()
(Ⅱ)求直线 ![]() 与平面
与平面 ![]() 所成的角的正弦值.
所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半圆AOB是某市休闲广场的平面示意图,半径OA的长为10,管理部门在A,B两处各安装好一个光源,其相应的光强度分别为4和9,根据光学原理,地面上某处照度y与光强度I成正比,与光源距离x的平方成反比,即y= ![]() (k为比例系数),经测量,在弧AB的中心C处的照度为130.(C处的照度为A,B两处光源的照度之和)
(k为比例系数),经测量,在弧AB的中心C处的照度为130.(C处的照度为A,B两处光源的照度之和) 
(1)求比例系数k的值;
(2)现在管理部门计划在半圆弧AB上,照度最小处增设一个光源P,试问新增光源P安装在什么位置?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com