
| A. | $\overrightarrow{{a_{10}}}$ | B. | $\overrightarrow{{a_{11}}}$ | C. | $\overrightarrow{{a_{20}}}$ | D. | $\overrightarrow{{a_{21}}}$ |
分析 可设每一项与前一项的差都等于向量$\overrightarrow{d}$,运用类似等差数列的通项和求和公式,计算可得$\overrightarrow{{S}_{21}}$=$\overrightarrow{{a}_{1}}+\overrightarrow{{a}_{2}}+$…+$\overrightarrow{{a}_{21}}$=21($\overrightarrow{{a}_{1}}$+10$\overrightarrow{d}$)=21$\overrightarrow{{a}_{11}}$,再由向量共线定理,即可得到所求结论.
解答 解:由新定义可设每一项与前一项的差都等于向量$\overrightarrow{d}$,
$\overrightarrow{{S}_{21}}$=$\overrightarrow{{a}_{1}}+\overrightarrow{{a}_{2}}+$…+$\overrightarrow{{a}_{21}}$
=$\overrightarrow{{a}_{1}}+(\overrightarrow{{a}_{1}}+\overrightarrow{d})+…+(\overrightarrow{{a}_{1}}+20\overrightarrow{d})$
=21$\overrightarrow{{a}_{1}}$+$\frac{1}{2}(1+20)•20\overrightarrow{d}$
=21($\overrightarrow{{a}_{1}}+10\overrightarrow{d}$)
=21$\overrightarrow{{a}_{11}}$,
∴一定平行$\overrightarrow{{S}_{21}}$的向量是$\overrightarrow{{a}_{11}}$.
故选:B.
点评 本题考查新定义:等差向量列的理解和运用,考查类比的思想方法和向量共线定理的运用,属于中档题.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 2 | C. | -2 | D. | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
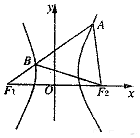 如图,F1,F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点,过F1的直线l与双曲线分别交于点A,B,且A(1,$\sqrt{3}$),若△ABF2为等边三角形,则△BF1F2的面积为( )
如图,F1,F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点,过F1的直线l与双曲线分别交于点A,B,且A(1,$\sqrt{3}$),若△ABF2为等边三角形,则△BF1F2的面积为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
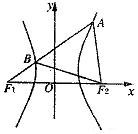 如图,F1,F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点,过F1的直线l与双曲线分别交于点A,B,若△ABF2为等边三角形,则双曲线的渐近线的斜率为( )
如图,F1,F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点,过F1的直线l与双曲线分别交于点A,B,若△ABF2为等边三角形,则双曲线的渐近线的斜率为( )| A. | ±$\sqrt{3}$ | B. | ±2 | C. | $±\sqrt{6}$ | D. | ±$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{10}$ | B. | 2$\sqrt{2}$ | C. | $\sqrt{6}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com