Question

已知（x+m）²ⁿ⁺¹与（mx+1）²ⁿ（n∈N^*，m≠0）的展开式中含xⁿ项的系数相等，求实数m的取值范围．

Answer 1

【答案】分析：利用二项展开式的通项公式求出（x+m）²ⁿ⁺¹与（mx+1）²ⁿ（n∈N^*，m≠0）的展开式中含xⁿ项的系数，根据已知条件得到关于m，n的方程；分离出m看成关于n的函数，通过函数的单调性，求出m的范围．
解答：解：设（x+m）²ⁿ⁺¹的展开式为T_r+1，
则T_r+1=C_2n+1^rx^2n+1-rm^r，
令2n+1-r=n
得r=n+1，
所以xⁿ的系数为C_2n+1ⁿ⁺¹mⁿ⁺¹．
由C_2n+1ⁿ⁺¹mⁿ⁺¹=C_2nⁿmⁿ，
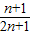
得m=是关于n的减函数，
∵n∈N⁺，
∴
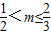
所以的取值范围是
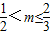点评：本题考查通过二项展开式的通项公式解决二项展开式的特定项问题，是一道基础题．