
做一个无盖的圆柱形水桶,若要使体积是27π,且用料最省,则圆柱的底面半径为 .
3
【解析】
试题分析:设圆柱的高为h,半径为r则由圆柱的体积公式可得,πr2h=27π,即 ,要使用料最省即求全面积的最小值,而S全面积=πr2+2πrh=
,要使用料最省即求全面积的最小值,而S全面积=πr2+2πrh= =
=
(法一)令S=f(r),结合导数可判断函数f(r)的单调性,进而可求函数取得最小值时的半径
(法二):S全面积=πr2+2πrh= =
= ,利用基本不等式可求用料最小时的r
,利用基本不等式可求用料最小时的r
【解析】
设圆柱的高为h,半径为r
则由圆柱的体积公式可得,πr2h=27π

S全面积=πr2+2πrh= =
=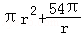
(法一)令S=f(r),(r>0)
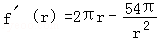 =
=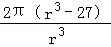
令f′(r)≥0可得r≥3,令f′(r)<0可得0<r<3
∴f(r)在(0,3)单调递减,在[3,+∞)单调递增,则f(r)在r=3时取得最小值
(法二):S全面积=πr2+2πrh=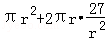 =
=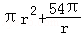
=
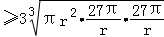 =27π
=27π
当且仅当 即r=3时取等号
即r=3时取等号
当半径为3时,S最小即用料最省
故答案为:3


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.2圆内接四边形性质与判定定理(解析版) 题型:填空题
(2014•泸州三模)在△ABC中,O是其外接圆的圆心,其两条中线的交点是G,两条高线的交点是H,设OG=λGH,则λ的值为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-2 2.2直接证明与间接证明练习卷(解析版) 题型:选择题
如果△A1B1C1的三个内角的余弦值分别等于△A2B2C2的三个内角的正弦值,则( )
A.△A1B1C1和△A2B2C2都是锐角三角形
B.△A1B1C1和△A2B2C2都是钝角三角形
C.△A1B1C1是钝角三角形,△A2B2C2是锐角三角形
D.△A1B1C1是锐角三角形,△A2B2C2是钝角三角形
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-1 3.4导数在实际生活中的应用练习卷(解析版) 题型:解答题
如图所示,设铁路AB=50,B、C之间距离为10,现将货物从A运往C,已知单位距离铁路费用为2,公路费用为4,问在AB上何处修筑公路至C,可使运费由A到C最省?

查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-1 3.4导数在实际生活中的应用练习卷(解析版) 题型:填空题
已知某生产厂家的年利润y(单位:万元)与年产量x(单位:万件)函数关系式为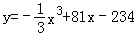 ,则使该生产厂家获取最大年利润的年产量为 .
,则使该生产厂家获取最大年利润的年产量为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-1 2.5圆锥曲线与方程练习卷(解析版) 题型:解答题
已知椭圆的两焦点为F1(0,﹣1)、F2(0,1),直线y=4是椭圆的一条准线.
(1)求椭圆方程;
(2)设点P在椭圆上,且|PF1|﹣|PF2|=1,求tan∠F1PF2的值.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-1 2.1圆锥曲线练习卷(解析版) 题型:选择题
设AB为过抛物线y2=2px(p>0)的焦点的弦,则|AB|的最小值为( )
A. B.P C.2P D.无法确定
B.P C.2P D.无法确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com