
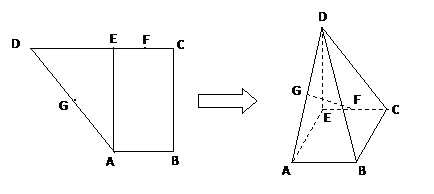
如图,已知直角梯形![]() 中,
中, ![]() 过
过![]()
作![]() ,垂足为
,垂足为![]() ,
,![]()
![]() 的中点,现将
的中点,现将![]() 沿
沿![]() 折叠,使得
折叠,使得![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:![]() ;
;
(Ⅲ)在线段![]() 上找一点
上找一点![]() ,使得面
,使得面![]() 面
面![]() ,并说明理由.
,并说明理由.
![]() ;
;![]() ;中点
;中点
(1)证明:由已知得:DE⊥AE,DE⊥EC,∴DE⊥面ABCE
∴DE⊥BC,又BC⊥CE,∴BC⊥面DCE
(2)证明:取AB中点H,连接GH,FH
∴GH‖BD, BD![]() 面BCD, GH
面BCD, GH![]() 面BCD
面BCD
∴GH‖面BCD
同理FH‖面BCD
∴面FHG‖面BCD ∴GF‖面BCD
(3)分析可知,R点满足3AR=RE时,面BDR⊥面BDC
证明:取BD中点Q,连结DR、BR、CR、CQ、RQ
![]() 容易计算CD=2,BD=,CR=,DR=
容易计算CD=2,BD=,CR=,DR=![]() ,CQ=
,CQ=![]()
在▲BDR中∵BR=,DR=![]() ,BD=
,BD=![]() ,可知RQ=
,可知RQ=
∴在▲CRQ中,CQ2+RQ2=CR2,∴CQ⊥RQ
又在▲CBD中,CD=CB,Q为BD中点∴CQ⊥BD.
∴CQ⊥面BDR,∴面BDC⊥面BDR


科目:高中数学 来源:高三数学教学与测试 题型:044
如图,已知直角梯形ABCD中,AB⊥BC,AB=AD=a,BC=3a,E是BC边上一动点,以DE为棱把△CDE折起,使其成直二面角C-DE-A,求四棱锥C-ABED体积的最大值.
查看答案和解析>>
科目:高中数学 来源:2014届河北省高一下学期期末数学试卷(解析版) 题型:解答题
(本小题共12分)
如图,已知四棱锥 中,
中,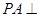 底面
底面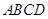 ,四边形
,四边形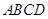 是直角梯形,
是直角梯形,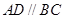 ,
,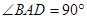 ,
,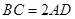 ,
,

(1)证明: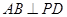 ;
;
(2)在线段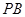 上找出一点
上找出一点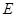 ,使
,使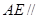 平面
平面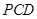 ,
,
指出点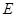 的位置并加以证明;
的位置并加以证明;
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分13分)
如图,已知直角梯形![]() 中,
中, ![]() 过
过![]()
作![]() ,垂足为
,垂足为![]() ,
,![]()
![]() 的中点,现将
的中点,现将![]() 沿
沿![]() 折叠,使得
折叠,使得![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:![]() ;
;
(Ⅲ)在线段![]() 上找一点
上找一点![]() ,使得面
,使得面![]() 面
面![]() ,并说明理由.
,并说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分13分)
如图,已知直角梯形![]() 中,
中, ![]() 过
过![]()
作![]() ,垂足为
,垂足为![]() ,
,![]()
![]() 的中点,现将
的中点,现将![]() 沿
沿![]() 折叠,使得
折叠,使得![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:![]() ;
;
(Ⅲ)在线段![]() 上找一点
上找一点![]() ,使得面
,使得面![]() 面
面![]() ,并说明理由.
,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com