Question

16．在Rt△ABC中，AB为斜边，AC=3，BC=4，P是中线CD上一点，设CP=x，记△APB的面积为y，则y关于x的解析式为y=1.2（5-2x）（0≤x＜2.5）．

Answer 1

分析 求△APB的面积为y，关键是求出△PAB边AB上的高．

解答 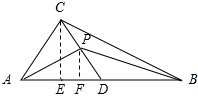解：由C点作斜边AB的垂线CE交AB于E（即Rt△ABC斜边上的高）
由P点作斜边AB的垂线PF交AB于F（即△PAB边AB上的高）
因为Rt△ABC中，∠ACB=90°，AC=3，BC=4，所以AB=5（勾股定理）
因为CD是Rt△ABC斜边上的中线，所以CD=$\frac{1}{2}$AB=2.5
因为△ACE∽△ABC，所以AC：AB=CE：BC，即$\frac{3}{5}=\frac{CE}{4}$，CE=$\frac{12}{5}$
因为△DPF∽△DCE，所以PF：CE=PD：CD
设PC=x，则PD=CD-x=2.5-x，所以PF=PD×CE÷CD=（2.5-x）×12÷（2.5×5）=（30-12x）÷12.5
所以S_△PAB=y=$\frac{1}{2}$AB×PF=5×（30-12x）÷12.5÷2
即：y=1.2（5-2x）．
故答案为：y=1.2（5-2x）（0≤x＜2.5）．

点评 本题考查三角形面积的计算，考查直角三角形的性质，关键是求出△PAB边AB上的高．