
����Ŀ���Ķ�������ϣ��������̽������y=x2�� ![]() ��ͼ��д��ͼ����������������õ��Ľ��ۣ����Բ²�����������Ӧ��ͼ�� �Ķ����ϣ�
��ͼ��д��ͼ����������������õ��Ľ��ۣ����Բ²�����������Ӧ��ͼ�� �Ķ����ϣ�
�ҹ�������ѧ�һ���������˵����ȱ��ʱ��ֱ�ۣ�������ʱ���������ν�ϰٰ�ã����ѷּ������ݣ�
����ѧ��ѧϰ���о��У����ú�����ͼ�����о����������ʣ�Ҳ���ú����Ľ���ʽ����ĥ������ͼ�����������������һ��Ӧ�ú����������о���Ӧͼ����״�����ӣ�
���ں���y= ![]() �����ǿ���ͨ������ʽ���о�����ͼ������ʣ��磺
�����ǿ���ͨ������ʽ���о�����ͼ������ʣ��磺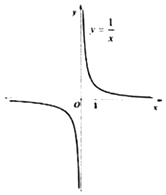
��1���ں���y= ![]() �У���x��0�������Ʋ������Ӧ��ͼ����y�ᣬ��ͼ����y��ཻ����y��0�������Ʋ������Ӧ��ͼ����x�ᣬ��ͼ����x��ཻ��
�У���x��0�������Ʋ������Ӧ��ͼ����y�ᣬ��ͼ����y��ཻ����y��0�������Ʋ������Ӧ��ͼ����x�ᣬ��ͼ����x��ཻ��
��2���ں���y= ![]() �У���x��0ʱy��0����x��0ʱy��0�������Ʋ������Ӧ��ͼ��ֻ���ڵ�һ�������ޣ�
�У���x��0ʱy��0����x��0ʱy��0�������Ʋ������Ӧ��ͼ��ֻ���ڵ�һ�������ޣ�
��3���ں���y= ![]() �У���x�ʣ�0��+�ޣ���y��0���ҵ�x������ʱy��С�������Ʋ������Ӧ��ͼ��Խ����Խ����x���x�ʣ����ޣ�0������y��0���ҵ�x��Сʱy���������Ʋ������Ӧ��ͼ��Խ����Խ����x�
�У���x�ʣ�0��+�ޣ���y��0���ҵ�x������ʱy��С�������Ʋ������Ӧ��ͼ��Խ����Խ����x���x�ʣ����ޣ�0������y��0���ҵ�x��Сʱy���������Ʋ������Ӧ��ͼ��Խ����Խ����x�
��4���ɺ���y= ![]() ��֪f����x��=��f��x������y=
��֪f����x��=��f��x������y= ![]() ���溯���������Ʋ������Ӧ��ͼ�����ԭ��Գƣ� ����������ʣ����������y=
���溯���������Ʋ������Ӧ��ͼ�����ԭ��Գƣ� ����������ʣ����������y= ![]() ��Ӧ��ͼ����ͼ��ʾ�����������о��У����Ǽ��õ��˴����һ���˼�룬���õ��˷������۵�˼�룬�Ƚ����˾�̬������㣩���о����ֽ����˶�̬�������ԣ���˼����������������ѧ�о��Ĺ��̣������о���ѧ�ijɹ���
��Ӧ��ͼ����ͼ��ʾ�����������о��У����Ǽ��õ��˴����һ���˼�룬���õ��˷������۵�˼�룬�Ƚ����˾�̬������㣩���о����ֽ����˶�̬�������ԣ���˼����������������ѧ�о��Ĺ��̣������о���ѧ�ijɹ���
���𰸡�
��1���⣺��y=x2�� ![]() �У�x��0�������Ʋ������Ӧ��ͼ����y�ᣬ����y��ཻ��
�У�x��0�������Ʋ������Ӧ��ͼ����y�ᣬ����y��ཻ��
��2���⣺��y=0����x2�� ![]() =0�����x=��1�������Ʋ������Ӧ��ͼ����x�ཻ����������Ϊ��1��0���ͣ���1��0����
=0�����x=��1�������Ʋ������Ӧ��ͼ����x�ཻ����������Ϊ��1��0���ͣ���1��0����
��3���⣺��y=x2�� ![]() �У���0��x��1ʱ��
�У���0��x��1ʱ�� ![]() ��1��x2����y��0����x��1ʱ��
��1��x2����y��0����x��1ʱ�� ![]() ��1��x2����y��0�������Ʋ������Ӧ��ͼ�������䣨0��1����ͼ����x����·��������䣨1��+�ޣ���ͼ����x����Ϸ�
��1��x2����y��0�������Ʋ������Ӧ��ͼ�������䣨0��1����ͼ����x����·��������䣨1��+�ޣ���ͼ����x����Ϸ�
��4���⣺��y=x2�� ![]() �У���x�ʣ�0��+�ޣ�����
�У���x�ʣ�0��+�ޣ�����
��x������ʱ ![]() ��С��x2��
��С��x2�� ![]() ��������y����������ԭ�����ڣ�0��+�ޣ�����������
��������y����������ԭ�����ڣ�0��+�ޣ�����������
�����Ʋ������Ӧ��ͼ��Խ���������ߣ��ǵ�������������
�ɺ���y=x2�� ![]() ��֪f����x��=f��x����������Ϊż�����������Ʋ������Ӧ��ͼ�����y��Գ�
��֪f����x��=f��x����������Ϊż�����������Ʋ������Ӧ��ͼ�����y��Գ�
��������ͨ�������Ķ���������x�Ľ��������yֵ�ı仯���ƣ���������ż�Ժͺ����ĵ����ԣ����ɺ��������ʼ��ɣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڶ�����ABCDE�У���BAC=90�㣬AB=AC=2��CD=2AE=2��AE��CD����AE�͵���ABC��FΪBC���е㣮 
��1����֤��AF��BD��
��2��������A��BE��D������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ��Ħ���ֵİ뾶Ϊ8m��ÿ12min��תһ�ܣ���͵������Ϊ2m����Ħ���ֱ�Եij��P����͵㰴��ʱ�뷽��ʼ��ת�����P�����ľ���h��m����ʱ��t��min��֮��ĺ�����ϵ�ǣ� �� 
A.h=8cost+10
B.h=��8cos ![]() t+10
t+10
C.h=��8sin ![]() t+10
t+10
D.h=��8cos ![]() t+10
t+10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ں���f��x����������ڷ��㳣��T��ʹ�õ�xȡ�������ڵ�ÿһ��ֵʱ������f��x+T��=f��x������ô����f��x���ͽ������ں�������֪����y=f��x����x��R������f��x+2��=f��x������x��[��1��1]ʱ��f��x��=x2 �� ��y=f��x����y=log5x��ͼ��Ľ������Ϊ�� ��
A.3
B.4
C.5
D.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������˵����
�ٴ�ֱ��ͬһƽ�����������һ�����棻
���ڡ�ABC�У���֪ ![]() �����A=60�㣻
�����A=60�㣻
���ڡ�ABC�У�sin2A=sin2B+sin2C+sinBsinC����A= ![]()
����a��0��b��0��a+b=2����a2+b2��2��
��ȷ������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����y=f��x���Ƕ�����R�ϵ�ż��������f��1+x��=f��1��x������0��x��1ʱ��f��x��=2��x �� ��f��3��= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��DE��BC��BC=2DE��CA��CB��CA��CD��CB��CD��F��G�ֱ���AC��BC�е㣮 
��1����֤��ƽ��DFG��ƽ��ABE��
��2����AC=2BC=2CD=4��������E��AB��C������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ������ϵx��Oy���ڵ�ƽ��Ϊ�£�ֱ������ϵxOy���ڵ�ƽ��Ϊ�����Ҷ���Ǧ���y�ᩁ�µĴ�С����30�㣮��֪���ڵ�����C��ķ�����3��x��2 ![]() ��2+4y2��36=0��������C���ڦ��ڵ���Ӱ������ϵxOy�µ����߷����� ��
��2+4y2��36=0��������C���ڦ��ڵ���Ӱ������ϵxOy�µ����߷����� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ABCD��A1B1C1D1�У�AA1�͵���ABCD����ADC=90�㣬AB��CD��AD=CD=DD1=2AB=2�� ���� ��֤��AD1��B1C��
���� ������A1��BD��C1������ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com