
等差数列{an}中,2a1+3a2=11,2a3=a2+a6-4,其前n项和为Sn.
(1)求数列{an}的通项公式.
(2)设数列{bn}满足bn=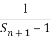 ,其前n项和为Tn,求证:Tn<
,其前n项和为Tn,求证:Tn< (n∈N*).
(n∈N*).
(1) an=2n-1 (2)见解析
【解析】(1)2a1+3a2=2a1+3(a1+d)=5a1+3d=11,
2a3=a2+a6-4,
即2(a1+2d)=a1+d+a1+5d-4,得d=2,
则a1=1,故an=2n-1.
(2)由(1)得Sn=n2,∴bn=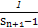 =
=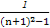
=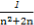 =
=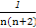 =
=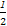 (
(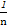 -
- ),
),
Tn=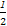 (
(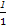 -
-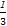 +
+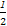 -
-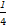 +
+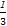 -
-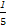 +…+
+…+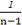 -
-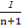 +
+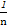 -
- )
)
=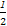 (
(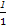 +
+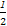 -
-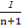 -
- )<
)<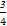 (n∈N*).
(n∈N*).
【方法技巧】裂项相消法的应用技巧
裂项相消法的基本思想是把数列的通项an分拆成an=bn+1-bn或者an=bn-bn+1或者an=bn+2-bn等,从而达到在求和时逐项相消的目的,在解题中要善于根据这个基本思想变换数列an的通项公式,使之符合裂项相消的条件.在裂项时一定要注意把数列的通项分拆成的两项一定是某个数列中的相邻的两项或者是等距离间隔的两项,只有这样才能实现逐项相消后剩下几项,达到求和的目的.


科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十六第六章第二节练习卷(解析版) 题型:选择题
函数f(x)=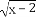 -
-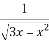 的定义域是( )
的定义域是( )
(A){x|2≤x≤3} (B){x|2≤x<3}
(C){x|0<x<3} (D){x|x>3}
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十九第六章第五节练习卷(解析版) 题型:选择题
若在曲线f(x,y)=0上存在两个不同点处的切线重合,则称这条切线为曲线f(x,y)=0的“自公切线”.下列方程:①x2-y2=1;②y=x2-|x|;③y=3sinx+4cosx;④|x|+1=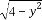 对应的曲线中存在“自公切线”的有( )
对应的曲线中存在“自公切线”的有( )
(A)①② (B)②③
(C)①④ (D)③④
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十九第六章第五节练习卷(解析版) 题型:选择题
已知f(x+1)= ,f(1)=1(x∈N*),猜想f(x)的表达式为( )
,f(1)=1(x∈N*),猜想f(x)的表达式为( )
(A)f(x)=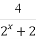 (B)f(x)=
(B)f(x)=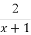
(C)f(x)=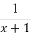 (D)f(x)=
(D)f(x)=
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十三第五章第四节练习卷(解析版) 题型:选择题
数列{an}的前n项和Sn=2n-1,则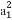 +
+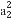 +
+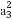 +…+
+…+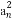 等于( )
等于( )
(A)(2n-1)2(B) (2n-1)2
(2n-1)2
(C)4n-1(D) (4n-1)
(4n-1)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十三第五章第四节练习卷(解析版) 题型:选择题
已知数列{an},若点(n,an)(n∈N*)在经过点(5,3)的定直线l上,则数列{an}的前9项和S9=( )
(A)9(B)10(C)18(D)27
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十一第五章第二节练习卷(解析版) 题型:解答题
数列{an}满足a1=1,an+1=(n2+n-λ)an(n=1,2,…),λ是常数.
(1)当a2=-1时,求λ及a3的值.
(2)数列{an}是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十六选修4-2第三节练习卷(解析版) 题型:解答题
已知y=f(x)的图象(如图1)经A=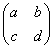 作用后变换为曲线C(如图2).
作用后变换为曲线C(如图2).
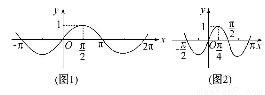
(1)求矩阵A. (2)求矩阵A的特征值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com