
【题目】如图,在直三棱柱ABC—A1B1C1中,AB=BC=BB1, ![]() ,D为AC上的点,B1C∥平面A1BD;
,D为AC上的点,B1C∥平面A1BD;
(1)求证:BD⊥平面![]() ;
;
(2)若![]() 且
且![]() ,求三棱锥A-BCB1的体积.
,求三棱锥A-BCB1的体积.

【答案】(1)见解析;(2)![]()
【解析】【试题分析】(1)运用线面垂直判定定理推证;(2)先求三棱锥的高与底面面积再运用三棱锥的体积公式求解:
(1)连结ED,
∵平面AB1C∩平面A1BD=ED,B1C∥平面A1BD,
∴B1C∥ED,
∵E为AB1中点,∴D为AC中点,
∵AB=BC, ∴BD⊥AC①

【法一】:由A1A⊥平面ABC, ![]() 平面ABC,得A1A⊥BD②,
平面ABC,得A1A⊥BD②,
由①②及A1A、AC是平面![]() 内的两条相交直线,得BD⊥平面
内的两条相交直线,得BD⊥平面![]() .
.
【法二】:由A1A⊥平面ABC,A1A![]() 平面
平面![]()
∴平面![]() ⊥平面ABC ,又平面
⊥平面ABC ,又平面![]()
![]() 平面ABC=AC,得BD⊥平面
平面ABC=AC,得BD⊥平面![]() .
.
(2)由![]() 得BC=BB1=1,
得BC=BB1=1,
由(1)知![]() ,又
,又![]() 得
得![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]()


科目:高中数学 来源: 题型:
【题目】如图所示,在四边形ABCD中,AB⊥DA,CE= ![]() ,∠ADC=
,∠ADC= ![]() ;E为AD边上一点,DE=1,EA=2,∠BEC=
;E为AD边上一点,DE=1,EA=2,∠BEC= ![]()
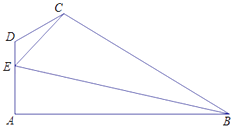
(1)求sin∠CED的值;
(2)求BE的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“累积净化量![]() ”是空气净化器质量的一个重要衡量指标,它是指空气净化从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示,根据
”是空气净化器质量的一个重要衡量指标,它是指空气净化从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示,根据![]() 《空气净化器》国家标准,对空气净化器的累计净化量
《空气净化器》国家标准,对空气净化器的累计净化量![]() 有如下等级划分:
有如下等级划分:
累积净化量(克) |
|
|
| 12以上 |
等级 |
|
|
|
|
为了了解一批空气净化器(共5000台)的质量,随机抽取![]() 台机器作为样本进行估计,已知这
台机器作为样本进行估计,已知这![]() 台机器的累积净化量都分布在区间
台机器的累积净化量都分布在区间![]() 中,按照
中,按照![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 均匀分组,其中累积净化量在
均匀分组,其中累积净化量在![]() 的所有数据有:4.5,4.6,5.2,5.3,5.7和5.9,并绘制了频率分布直方图,如图所示:
的所有数据有:4.5,4.6,5.2,5.3,5.7和5.9,并绘制了频率分布直方图,如图所示:
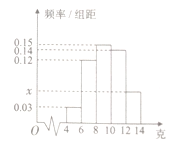
(1)求![]() 的值及频率分布直方图中
的值及频率分布直方图中![]() 的值;
的值;
(2)以样本估计总体,试估计这批空气净化器(共5000台)中等级为![]() 的空气净化器有多少台?
的空气净化器有多少台?
(3)从累积净化量在![]() 的样本中随机抽取2台,求恰好有1台等级为
的样本中随机抽取2台,求恰好有1台等级为![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=x3+2x2﹣4x+5在[﹣4,1]上的最大值和最小值分别是( )
A.13, ![]()
B.4,﹣11
C.13,﹣11
D.13,最小值不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
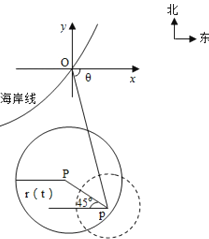
【题目】在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南![]() 方向
方向![]() 的海面P处,且
的海面P处,且![]() ,并以
,并以![]() 的速度向西偏北
的速度向西偏北![]() 方向移动,台风侵袭的范围为圆形区域,当前半径为
方向移动,台风侵袭的范围为圆形区域,当前半径为![]() ,并以
,并以![]() 的速度不断增大,问几小时后该城市开始受到台风的侵袭?
的速度不断增大,问几小时后该城市开始受到台风的侵袭?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△OAB的顶点坐标为O(0,0),A(2,9),B(6,﹣3),点P的横坐标为14,且 ![]() =λ
=λ ![]() ,点Q是边AB上一点,且
,点Q是边AB上一点,且 ![]()
![]() =0.
=0.
(1)求实数λ的值与点P的坐标;
(2)求点Q的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=6,BD=8,E是PB上任意一点,△AEC面积的最小值是3.
(Ⅰ)求证:AC⊥DE;
(Ⅱ)求四棱锥P﹣ABCD的体积.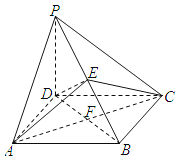
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com