
如图,在平面直角坐标系 中,已知
中,已知 ,
, ,
, 是椭圆
是椭圆 上不同的三点,
上不同的三点, ,
, ,
, 在第三象限,线段
在第三象限,线段 的中点在直线
的中点在直线 上.
上.

(1)求椭圆的标准方程;
(2)求点C的坐标;
(3)设动点 在椭圆上(异于点
在椭圆上(异于点 ,
, ,
, )且直线PB,PC分别交直线OA于
)且直线PB,PC分别交直线OA于 ,
, 两点,证明
两点,证明 为定值并求出该定值.
为定值并求出该定值.
(1)求椭圆方程一般用待定系数法.本题已知椭圆过两点,列两个方程 ,解出
,解出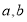 的值,(2)求点
的值,(2)求点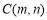 的坐标,需列出两个方程.一是点C在椭圆上,即
的坐标,需列出两个方程.一是点C在椭圆上,即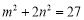 ,二是
,二是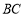 的中点在直线
的中点在直线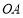 上,即
上,即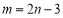 .注意到
.注意到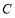 在第三象限,舍去正值.(3)题意明确,思路简洁,就是求出点
在第三象限,舍去正值.(3)题意明确,思路简洁,就是求出点 的坐标,算出
的坐标,算出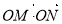 为定值.难点是如何消去参数.因为点
为定值.难点是如何消去参数.因为点 在直线
在直线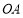 :
:  上,所以可设
上,所以可设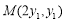 ,
,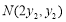 .选择
.选择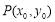 作为参数,即用
作为参数,即用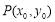 表示点
表示点 的坐标.由
的坐标.由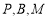 三点共线,解得
三点共线,解得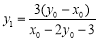 ,同理解得
,同理解得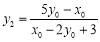 .从而有
.从而有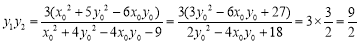 ,这里主要用到
,这里主要用到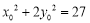 代入化简.本题也可利用椭圆参数方程或三角表示揭示
代入化简.本题也可利用椭圆参数方程或三角表示揭示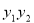 为定值.
为定值.
【解析】
试题分析:(1) ,(2)
,(2)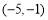 ,(3)
,(3)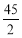 .
.
试题解析:(1)由已知,得 解得
解得 2分
2分
所以椭圆的标准方程为 . 3分
. 3分
(2)设点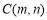
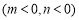 ,则
,则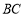 中点为
中点为 .
.
由已知,求得直线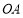 的方程为
的方程为 ,从而
,从而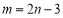 .①
.①
又∵点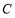 在椭圆上,∴
在椭圆上,∴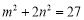 .②
.②
由①②,解得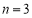 (舍),
(舍),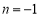 ,从而
,从而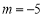 . 5分
. 5分
所以点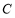 的坐标为
的坐标为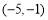 . 6分
. 6分
(3)设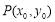 ,
,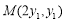 ,
,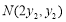 .
.
∵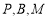 三点共线,∴
三点共线,∴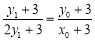 ,整理,得
,整理,得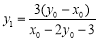 . 8分
. 8分
∵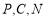 三点共线,∴
三点共线,∴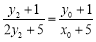 ,整理,得
,整理,得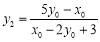 . 10分
. 10分
∵点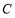 在椭圆上,∴
在椭圆上,∴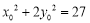 ,
,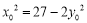 .
.
从而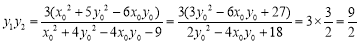 . 14分
. 14分
所以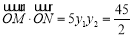 . 15分
. 15分
∴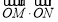 为定值,定值为
为定值,定值为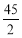 . 16分
. 16分
考点:椭圆标准方程,直线与椭圆位置关系


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源:2013-2014学年江苏省连云港市高三3月第二次调研考试理科数学试卷(解析版) 题型:填空题
从甲,乙,丙,丁4个人中随机选取两人,则甲乙两人中有且只有一个被选取的概率为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省苏、锡、常、镇四市高三教学情况调查(一)文科数学试卷(解析版) 题型:填空题
已知函数
 ,若函数
,若函数 恰有两个不同的零点,则实数
恰有两个不同的零点,则实数 的取值范围为 .
的取值范围为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省盐城市高三第三次模拟考试数学试卷(解析版) 题型:解答题
在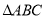 中,角
中,角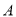 ,
, ,
,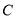 的对边分别为
的对边分别为 ,
,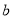 ,
,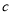 ,若
,若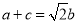 .
.
(1)求证: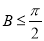 ;
;
(2)当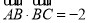 ,
,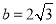 时,求
时,求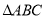 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省淮安市高三5月信息卷文科数学试卷(解析版) 题型:解答题
已知函数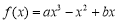 (
(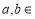 R),
R),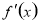 为其导函数,且
为其导函数,且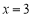 时
时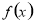 有极小值
有极小值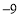 .
.
(1)求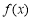 的单调递减区间;
的单调递减区间;
(2)若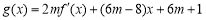 ,
,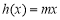 ,当
,当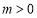 时,对于任意x,
时,对于任意x,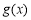 和
和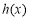 的值至少有一个是正数,求实数m的取值范围;
的值至少有一个是正数,求实数m的取值范围;
(3)若不等式 (
(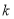 为正整数)对任意正实数
为正整数)对任意正实数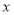 恒成立,求
恒成立,求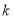 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com