练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图2-5-17，PA切⊙O于A，PCB、PDE为⊙O的割线，并且PDE过圆心O，已知∠BPA=30°，PA=23，PC=1，求PD的长.

    图2-5-17

    思路分析:求PD，可使用割线定理PC·PB=PD·PE，显然PA切⊙O，

    ∴PA2=PC·PB.

    可求得PB，但PE=PD＋DE，DE为⊙O直径，所以求⊙O的直径成为解题的关键.

    解:∵PA切⊙O，∴PA2=PC·PB.

    又PB=PC＋BC，∴BC=11.

    连结AO，并延长与⊙O交于K，与CB交于G，则GA=PAtan∠GPA=PAtan30°=2.

    又Rt△GPA中，∠GPA=30°，

    ∴PG=2GA=4.∴CG=3，GB=8.

    由相交弦定理GC·GB=AG·GK，可得GK=12，∴直径为14.

    ∴由割线定理有PC·PB=PD·PE，得PD=-7.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2011•开封一模）给出30个数2，3，5，8，12，17，…，要计算这30个数的和，该问题的程序框图如图：则框图中判断框①和执行框②应是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：013

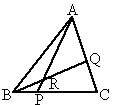
    如图所示，P、Q分别在BC和AC上，BP∶CP=2∶5，CQ∶QA=3∶4，则=

    [　　]

    A．3∶14

    B．14∶3

    C．17∶3

    D．17∶14

    查看答案和解析>>

    科目：高中数学 来源：2009-2010学年度新课标高三上学期数学单元测试8-文科-立体几何初步 题型：解答题

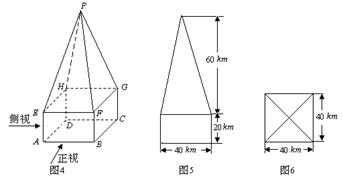
     (09广东文17)某高速公路收费站入口处的安全标识墩如图4所示,墩的上半部分是正四棱锥P－EFGH,下半部分是长方体ABCD－EFGH．图5、图6分别是该标识墩的正(主)视图和俯视图．

       （1）请画出该安全标识墩的侧(左)视图;

       （2）求该安全标识墩的体积

       （3）证明:直线BD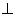平面PEG

     

     

     

    查看答案和解析>>

    科目：高中数学 来源：2011年河南省开封市高考数学一模试卷（理科）（解析版） 题型：选择题

    给出30个数2，3，5，8，12，17，…，要计算这30个数的和，该问题的程序框图如图：则框图中判断框①和执行框②应是（ ）

    A．i≤30，p=p+i-1
    B．i≤31，p=p+i+1
    C．i≤30，p=p+i
    D．i≤31，p=p+i

    查看答案和解析>>

    同步练习册答案