
 (2)若
(2)若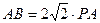 ,∠ABC=30°,求二面角A—PB—C的大小.
,∠ABC=30°,求二面角A—PB—C的大小. 设AB=2r,在Rt△ABC中,∠ABC=30°,所以AC=r
设AB=2r,在Rt△ABC中,∠ABC=30°,所以AC=r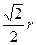
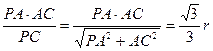
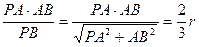
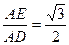 ,所以∠ADE=60°
,所以∠ADE=60°

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
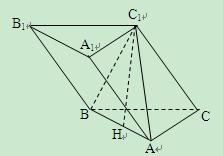
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
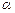 ,直线
,直线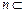 平面
平面 ,则下列命题正确的是 ( )
,则下列命题正确的是 ( )| A.若α∥β,则m⊥n | B.若α⊥β,则m∥n |
| C.若m⊥n,则α∥β | D.若n∥α,则α∥β |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
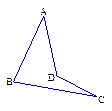
| A.点P必在直线AC上 | B.点P必在直线BD上 |
| C.点P必在平面DBC外 | D.点P必在平面ABC内 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
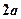 的正方体容器被水充满,首先把半径为
的正方体容器被水充满,首先把半径为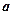 的球放入其中,再放入一个能被水完全淹没的小球,若想使溢出的水量最大,这个小球的半径为( )
的球放入其中,再放入一个能被水完全淹没的小球,若想使溢出的水量最大,这个小球的半径为( )A.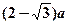 | B.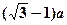 | C.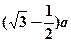 | D.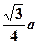 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com