分析:(1)利用两圆相外切的条件,结合双曲线的定义,求出双曲线的方程.
(2)①MD的最小值为c-a=1,且M(-1,0)写出方程.
②先求出点P坐标表达式,代入⊙M方程,求出点P的坐标,判断M0APB是菱形,求出AB斜率,及M0P的中点,点斜式写出直线l的方程.
解答:解:(1)圆C半径R=2,圆心C(2,0),(1分)由题意可得,MC=MD+2,MC-MD=2<CD=4,(3分)
∴点M的轨迹是以C,D为焦点的双曲线的左支,其中2a=2,2c=4,∴a=1,c=2,∴b
2=3.(5分)
∴点M的轨迹方程为
x2-=1(x<0).(6分)
(2)①∵MD的最小值为c-a=1,且M(-1,0),∴⊙M
0的方程为(x+1)
2+y
2=1.(8分)
②由
=(λ+1 , 3λ),把点P(λ,3λ)代入⊙M:(x+1)
2+y
2=1,
解得
λ=0(舍),-,(10分)∴
P(- , -),且
kM0P=-.(12分)
∵
=+,且
||=||=||=r,∴M
0APB是菱形. (13分)
∴
⊥,∴
kAB=-=.
又M
0P的中点为
(-,-),∴直线
l: y+=(x+),
即
4x-3y+=0.(15分)
点评:本题考查轨迹方程的求法,直线和圆位置关系的综合应用,属于中档题.



 轻松暑假总复习系列答案
轻松暑假总复习系列答案 已知椭圆C经过点M(1,
已知椭圆C经过点M(1,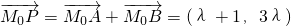 (λ≠0)
(λ≠0)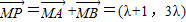 (λ≠0)
(λ≠0)