
【题目】己知抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,则直线
,则直线![]() 称为抛物线
称为抛物线![]() 的伴随直线.
的伴随直线.
(1)求抛物线![]() 的伴随直线的表达式;
的伴随直线的表达式;
(2)已知抛物线![]() 的伴随直线为
的伴随直线为![]() ,且该抛物线与
,且该抛物线与![]() 轴有两个不同的公共点,求
轴有两个不同的公共点,求![]() 的取值范围.
的取值范围.
(3)已知![]() ,若抛物线
,若抛物线![]() 的伴随直线为
的伴随直线为![]() ,且该抛物线与线段
,且该抛物线与线段![]() 恰有1个公共点,求
恰有1个公共点,求![]() 的取值范围(直接写出答案即可)
的取值范围(直接写出答案即可)
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3) ![]() 或
或![]() .
.
【解析】
(1)先求抛物线的顶点为![]() ,再与抛物线
,再与抛物线![]() 轴的交点为
轴的交点为![]() ,根据截距式即可得出伴随直线方程.
,根据截距式即可得出伴随直线方程.
(2)先求抛物线![]() 的顶点
的顶点![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,将
,将![]() 代入伴随直线
代入伴随直线![]() 方程,解得
方程,解得![]() ,
,![]() ,再根据该抛物线与
,再根据该抛物线与![]() 轴有两个不同的公共点,用根的判别式列不等式,解得
轴有两个不同的公共点,用根的判别式列不等式,解得![]() ,结合
,结合![]() ,即可得出
,即可得出![]() 的取值范围.
的取值范围.
(3)根据抛物线![]() 的伴随直线为
的伴随直线为![]() ,将抛物线化为
,将抛物线化为![]() ,又因为该抛物线与线段
,又因为该抛物线与线段![]() 恰有1个公共点,即则
恰有1个公共点,即则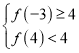 或
或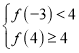 ,代入数据求解即可.
,代入数据求解即可.
解: (1)![]() 的顶点为
的顶点为![]() ,
,
与抛物线![]() 轴的交点为
轴的交点为![]() ,
,
直线![]() :
:![]() ,即
,即![]() ,
,
所以抛物线![]() 的伴随直线为:
的伴随直线为: ![]() .
.
(2)已知抛物线![]() 的伴随直线为
的伴随直线为![]() ,
,
顶点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,
,
![]() 在直线
在直线![]() 上,
上,
所以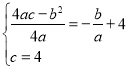 ,解得
,解得![]() ,
,
又因该抛物线与![]() 轴有两个不同的公共点,
轴有两个不同的公共点,
![]() ,所以
,所以![]() ,解得
,解得![]() ,
,
又因为![]() ,故
,故![]() 且
且![]() .
.
所以![]() 的取值范围为
的取值范围为![]() .
.
(3)因为抛物线![]() 的伴随直线为
的伴随直线为![]() ,
,
顶点![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,
,
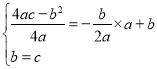 ,解得:
,解得:![]() ,
,
所以抛物线可表示为: ![]() ,对称轴为
,对称轴为![]()
又因为![]() ,
,
且该抛物线与线段![]() 恰有1个公共点
恰有1个公共点
线段![]() 为:
为:![]() .
.
则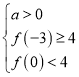 或
或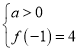
解得![]() 或
或![]() ,.
,.
所以可得![]() 的取值范围为
的取值范围为![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|![]() ),x
),x![]() 为f(x)的零点,x
为f(x)的零点,x![]() 为y=f(x)图象的对称轴,且f(x)在(
为y=f(x)图象的对称轴,且f(x)在(![]() )上单调,则ω的最大值为_____.
)上单调,则ω的最大值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题为真命题的是( )
A.若![]() 为真命题,则
为真命题,则![]() 为真命题;
为真命题;
B.“![]() ”是“
”是“![]() ”的充分不必要条件;
”的充分不必要条件;
C.命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”;
”;
D.已知命题![]() ,使得
,使得![]() ,则
,则![]() ,使得
,使得![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() ,定直线
,定直线![]() :
: ![]() ,动圆
,动圆![]() 过点
过点![]() ,且与直线
,且与直线![]() 相切.
相切.
(Ⅰ)求动圆![]() 的圆心轨迹
的圆心轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线与曲线
的直线与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,分别过点
两点,分别过点![]() ,
, ![]() 作曲线
作曲线![]() 的切线
的切线![]() ,
, ![]() ,两条切线相交于点
,两条切线相交于点![]() ,求
,求![]() 外接圆面积的最小值.
外接圆面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com