练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图所示，在杨辉三角中，斜线上方从1开始按箭头所示的数组成一个锯齿形数列1，3，3，4，6，5，10，…，记此数列为{an}，则a21=
    66
    66
    ．
    分析：由图中锯齿形数列排列，发现规律：奇数项的第n项可以表示成正整数的前n项和的形式，偶数项构成以3为首项，公差是1的等差数列．由此再结合等差数列的通项公式，即可得到a21的值．
    解答：解：根据图中锯齿形数列的排列，发现
    a1=1，a3=3=1+2，a5=6=1+2+3，…，
    ∴a21=1+2+3+…+11=
    (1+11)×11
    2
    =66．
    故答案为：66．
    点评：本题以杨辉三角为例，求锯齿形数列的前n项和，着重考查了等差数列的通项与求和公式和归纳推理的一般方法等知识点，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：013

    (2006潍坊模拟)如图所示，在杨辉三角中，斜线l的上方，从1开始按箭头所示的数组成一个锯齿形数列：1，3，3，4，6，5，10，…，记此数列为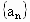，则等于

    [　　]

    A．55

    B．65

    C．66

    D．78

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：022

    如图所示，在杨辉三角中，从上往下共有n(nÎ N*)行，在这些数中排1的数字之和是________．

    查看答案和解析>>

    科目：高中数学 来源：2011届高考数学第一轮复习测试题11 题型：022

    如图所示，在杨辉三角中，斜线AB上方箭头所示的数组成一个锯齿形的数列：1，2，3，3，6，4，10，…记该数列前n项之和为S(n)，则S(16)＝________．

    查看答案和解析>>

    科目：高中数学 来源：2009-2010学年北京市丰台区高二（下）期末数学试卷（理科）（解析版） 题型：填空题

    如图所示，在杨辉三角中，斜线上方从1开始按箭头所示的数组成一个锯齿形数列1，3，3，4，6，5，10，…，记此数列为{an}，则a21=    ．

    查看答案和解析>>

    同步练习册答案