
分析 (1)由a2+a3=10,a1•a4=16,联立解方程组$\left\{\begin{array}{l}{{2a}_{1}+3d=10}\\{{{a}_{1}}^{2}+3{a}_{1}d=16}\end{array}\right.$,求得d和a1,求得数列{an}的通项公式;
(2)由题意可知n≥2时,an=$\frac{b_1}{3+1}+\frac{b_2}{{{3^2}+1}}+\frac{b_3}{{{3^3}+1}}+…+\frac{b_n}{{{3^n}+1}}$,an-1=$\frac{{b}_{1}}{3+1}$+$\frac{{b}_{2}}{{3}^{2}+1}$+$\frac{{b}_{3}}{{3}^{3}+1}$+…+$\frac{{b}_{n-1}}{{3}^{n-1}+1}$,两式相减2=$\frac{{b}_{n}}{{3}^{n}+1}$,求得bn的通项公式,当n=1时,验证是否满足;
(3)由(1),(2)代入求得数列{cn}的通项公式,利用“错位相减法”及等差数列前n项和公式即可求得数列{cn}的前n项和Tn.
解答 解:(1)数列{an}是递增的等差数列,d>0,
由题意可知:$\left\{\begin{array}{l}{{a}_{1}+d+{a}_{1}+2d=10}\\{{a}_{1}({a}_{1}+3d)=16}\end{array}\right.$,整理得:$\left\{\begin{array}{l}{{2a}_{1}+3d=10}\\{{{a}_{1}}^{2}+3{a}_{1}d=16}\end{array}\right.$,
解得$\left\{\begin{array}{l}{d=2}\\{{a}_{1}=2}\end{array}\right.$
数列{an}的通项公式an=2n;
(2)当n≥2时,an=$\frac{b_1}{3+1}+\frac{b_2}{{{3^2}+1}}+\frac{b_3}{{{3^3}+1}}+…+\frac{b_n}{{{3^n}+1}}$,
an-1=$\frac{{b}_{1}}{3+1}$+$\frac{{b}_{2}}{{3}^{2}+1}$+$\frac{{b}_{3}}{{3}^{3}+1}$+…+$\frac{{b}_{n-1}}{{3}^{n-1}+1}$,
两式相减得:2=$\frac{{b}_{n}}{{3}^{n}+1}$,
∴${b_n}=2({3^n}+1)$,
当n=1时,$\frac{{b}_{1}}{3+1}$=a1=2,b1=8,成立,
∴数列{bn}的通项公式数列{bn}的通项公式${b_n}=2({3^n}+1)$;
(3)${c_n}=\frac{{{a_n}{b_n}}}{4}=n({3^n}+1)=n•{3^n}+n$,
Tn=c1+c2+c3+…+cn
=(1×3+2×32+3×33+…+n×3n)+(1+2+3+…+n),
令${H_n}=1×3+2×{3^2}+3×{3^3}+…+n•{3^n}$
则$3{H_n}=1×{3^2}+2×{3^3}+3×{3^4}+…+n•{3^{n+1}}$
两式相减得:$-2{H_n}=3+{3^2}+{3^3}+…+{3^n}-n×{3^{n+1}}=\frac{{3({3^n}-1)}}{3-1}-n×{3^{n+1}}$,
∴${H_n}=\frac{{(2n-1)×{3^{n+1}}+3}}{4}$
∴${T_n}=\frac{{(2n-1)×{3^{n+1}}}}{4}+\frac{n(n+1)}{2}+\frac{3}{4}$.
点评 本题考查等差数列通项公式及前n项和公式,考查“错位相减法”求数列前n项和,考查分析问题及解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |a|>|b| | B. | lg(a-b)>0 | C. | ${({\frac{1}{2}})^a}<{({\frac{1}{2}})^b}$ | D. | 2a>3b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(3,+∞) | B. | (-3,1) | C. | (-∞,-3)∪(1,+∞) | D. | (-1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
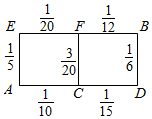 某人居住在城镇的A处,准备开车到单位B处上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图(例如A→C→D算两个路段:设路段AC发生堵车事件的概率为$\frac{1}{10}$,路段CD发生堵车事件的概率为$\frac{1}{15}$).
某人居住在城镇的A处,准备开车到单位B处上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图(例如A→C→D算两个路段:设路段AC发生堵车事件的概率为$\frac{1}{10}$,路段CD发生堵车事件的概率为$\frac{1}{15}$).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com