练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知实数，满足，实数，满足，则的最小值为__________．

    【答案】1

    【解析】由ln(b+1)+a3b=0,得a=3bln(b+1),则点(b,a)是曲线y=3xln(x+1)上的任意一点，

    由2dc =0,得c=2d ,则点(d,c)是直线y=2x 上的任意一点，

    因为(ac)2+(bd)2表示点(b,a)到点(d,c)的距离的平方，即曲线上的一点与直线上一点的距离的平方，

    所以(ac)2+(bd)2的最小值就是曲线上的点到直线距离的最小值的平方,即曲线上与直线y=2x 平行的切线到该直线的距离的平方。

    ，令y′=2，得x=0，此时y=0，即过原点的切线方程为y=2x，

    则曲线上的点到直线距离的最小值的平方d2= =1.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设首项为1的正项数列{an}的前n项和为Sn，且Sn＋1－3Sn＝1.

    (1) 求证：数列{an}为等比数列；

    (2) 数列{an}是否存在一项ak，使得ak恰好可以表示为该数列中连续r(r∈N*，r≥2)项的和？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】【湖南省2017届高三长郡中学、衡阳八中等十三校重点中学第一次联考数学（理）】

    已知函数.

    （1）当时，试求函数图像过点的切线方程；

    （2）当时，若关于的方程有唯一实数解，试求实数的取值范围；

    （3）若函数有两个极值点，且不等式恒成立，试求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数， ，其中

    （1）设函数，求函数的单调区间；

    （2）若存在，使得成立，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】齐王与田忌赛马，田忌的上等马优于齐王的中等马，劣于齐王的上等马，田忌的中等马优于齐王的下等马，劣于齐王的中等马,田忌的下等马劣于齐王的下等马，现从双方的马匹中随机选一匹进行一场比赛,则田忌马获胜的概率为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f(x)＝ln x－ax(a∈R)(e＝2.718 28…是自然对数的底数)．

    (1)判断f(x)的单调性；

    (2)当f(x)<0在(0，＋∞)上恒成立时，求a的取值范围；

    (3)证明：当x∈(0，＋∞)时， (1＋x) <e.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知椭圆： 的离心率为，以椭圆的左顶点为圆心作圆： ，设圆与椭圆交于点与点．

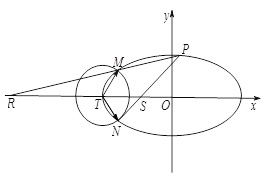
    （1）求椭圆的方程；

    （2）求的最小值，并求此时圆的方程；

    （3）设点是椭圆上异于, 的任意一点，且直线分别与轴交于点， 为坐标原点，求证： 为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）讨论函数在区间上的单调性；

    （2）若曲线仅在两个不同的点，处的切线都经过点，其中，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，函数 (a>0)，

    若存在，使得成立，则实数的取值范围是(　　)

    A. B. C. D.

    查看答案和解析>>

    同步练习册答案