
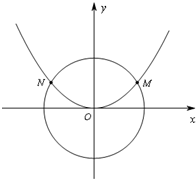
如图,已知抛物线C1:x2=2py(p>0)与圆C2:x2+y2=![]() 交于M、N两点,且∠MON=120°.
交于M、N两点,且∠MON=120°.
(1)求抛物线C1的方程;
(2)设直线l与圆C2相切.
①若直线l与抛物线C1也相切,求直线l的方程.
②若直线l与抛物线C1交于不同的A、B两点,求![]() ·
·![]() 的取值范围.
的取值范围.
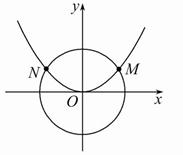
(1)因为∠MON=120°,所以OM与x轴正半轴成30°角,所以点M的坐标为(![]() ,
,![]() ),代入抛物线方程得(
),代入抛物线方程得(![]() )2=2p×
)2=2p×![]() ,求得p=1,
,求得p=1,
所以抛物线C1的方程为x2=2y.
(2)由题意可设l:y=kx+b,即kx-y+b=0,
因为l与圆C2相切,所以![]() =
=![]() ,
,
即9b2=16(k2+1) (Ⅰ)
①设直线l与抛物线C1:x2=2y即y=![]() x2相切于点T(t,
x2相切于点T(t,![]() t2),因为函数y=
t2),因为函数y=![]() x2的导数为y′=x,所以
x2的导数为y′=x,所以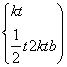 (Ⅱ)
(Ⅱ)
由(Ⅰ)、(Ⅱ)解得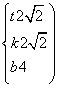 或
或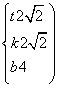
所以直线l的方程为y=-2![]() x-4或y=2
x-4或y=2![]() x-4.
x-4.
②由![]() 得x2-2kx
得x2-2kx![]() -2b=0,
-2b=0,
设A(x1,y1),B(x2,y2),
则x1+x2=2k,x1x2=-2b,且由Δ=4k2+8b>0得k2+2b>0 (Ⅲ)
由(Ⅰ)、(Ⅲ)可得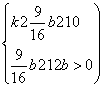 ,解得b≥
,解得b≥![]() 或b<-4,
或b<-4,
所以![]() ·
·![]() =x1x2+y1y2=
=x1x2+y1y2=![]() (x1x2)2+x1x2=b2-2b∈[-
(x1x2)2+x1x2=b2-2b∈[-![]() ,+∞),即
,+∞),即![]() ·
·![]() 的取值范围是[-
的取值范围是[-![]() ,+∞).
,+∞).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 (2013•嘉兴二模)如图,已知抛物线C1:x2=2py的焦点在抛物线C2:y=
(2013•嘉兴二模)如图,已知抛物线C1:x2=2py的焦点在抛物线C2:y=| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•嘉兴二模)如图,已知抛物线C1:x2=2py的焦点在抛物线C2:y=
(2013•嘉兴二模)如图,已知抛物线C1:x2=2py的焦点在抛物线C2:y=| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知抛物线C1:x2=2py(p>0)与圆C2:x2+y2=
如图,已知抛物线C1:x2=2py(p>0)与圆C2:x2+y2=| 16 |
| 9 |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源:2014届江西吉安二中高二月考文科数学试卷(解析版) 题型:解答题
(14分)如图,已知抛物线C1: y=x2, 与圆C2: x2+(y+1)2="1," 过y轴上一点A(0, a)(a>0)作圆C2的切线AD,切点为D(x0, y0).

(1)证明:(a+1)(y0+1)=1
(2)若切线AD交抛物线C1于E,且E为AD的中点,求点A纵坐标a.
查看答案和解析>>
科目:高中数学 来源:2011年福建省南平市高三适应性考试数学试卷(理科)(解析版) 题型:解答题
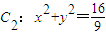 交于M、N两点,
交于M、N两点,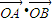 的取值范围.
的取值范围.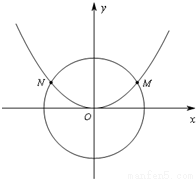
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com