练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    某校高一年级名学生参加数学竞赛，成绩全部在分至分之间，现将成绩分成以下段：
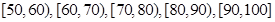    ，据此绘制了如图所示的频率分布直方图.

    （1）求成绩在区间的频率；
    （2）从成绩大于等于分的学生中随机选名学生，其中成绩在内的学生人数为，求的分布列与均值.

    （1）；（2）.

    解析试题分析：（1）根据频率分布直方图可知成绩在区间的频率为；（2）由已知和（1）的结果可知成绩在区间内的学生有人，成绩在区间内的学生有人，那么的所有可能取值为，然后求出所对应的概率分别为：
    ，列出分布列后求出的数学期望为：=
    试题解析：（1）根据频率分布直方图可知成绩在区间的频率为；
    （2）由已知和（1）的结果可知成绩在区间内的学生有人，成绩在区间内的学生有人， 依题意，可能取的值为.
    则：
    所以的分布列为：


    		0
    		1
    		2
    		3
    P




    则均值=
    考点：频率分布直方图，离散型随机变量的分布列与数学期望.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    城市公交车的数量若太多则容易造成资源的浪费；若太少又难以满足乘客需求.某市公交公司在某站台的60名候车乘客中随机抽取15人，将他们的候车时间作为样本分成5组，如下表所示（单位：分钟）：

    组别
    		候车时间
    		人数
    一
    		 
    		2
    二

    		6
    三

    		4
    四

    		2
    五

    		1
    （1）估计这60名乘客中候车时间少于10分钟的人数；
    （2）若从上表第三、四组的6人中任选2人作进一步的调查，求抽到的两人恰好来自不同组的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某校高三某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下图,据此解答如下问题:

    (1)求分数在[50,60)的频率及全班的人数.
    (2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高.
    (3)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份在[90,100]之间的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某地粮食需求量逐年上升,下表是部分统计数据:

    年份(年)
    		2002
    		2004
    		2006
    		2008
    		2010
    需求量
    (万吨)
    		236
    		246
    		257
    		276
    		286
    (1)利用所给数据求年需求量与年份之间的回归直线方程=x+.
    (2)利用(1)中所求出的直线方程预测该地2014年的粮食需求量.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某高校组织自主招生考试，共有2 000名优秀同学参加笔试，成绩均介于195分到275分之间，从中随机抽取50名同学的成绩进行统计，将统计结果按如下方式分成8组：第1组[195,205)，第2组[205,215)，…，第8组[265,275]．如图是按上述分组方法得到的频率分布直方图，且笔试成绩在260分(含260分)以上的同学进入面试．

    (1)估计所有参加笔试的2 000名同学中，参加面试的同学人数；
    (2)面试时，每位同学抽取两个问题，若两个问题全答错，则不能取得该校的自主招生资格；若两个问题均回答正确且笔试成绩在270分以上，则获A类资格；其他情况下获B类资格．现已知某中学有两人获得面试资格，且仅有一人笔试成绩为270分以上，在回答两个面试问题时，两人对每一个问题正确回答的概率均为，求恰有一名同学获得该高校B类资格的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    汽车是碳排放量比较大的行业之一，某地规定，从2014年开始，将对二氧化碳排放量超过的轻型汽车进行惩罚性征税。检测单位对甲、乙两品牌轻型汽车各抽取5辆进行二氧化碳排放量检测，记录如下（单位：）.

    经测算得乙品牌轻型汽车二氧化碳排放量的平均值为.
    （1）从被检测的5辆甲品牌轻型汽车中任取2辆，则至少有一辆二氧化碳排放量超过的概率是多少？
    （2）求表中的值，并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    经销商经销某种农产品，在一个销售季度内，每售出1 t该产品获利润500元，未售出的产品，每1 t亏损300元．根据历史资料，得到销售季度内市场需求量的频率分布直方图，如图所示．经销商为下一个销售季度购进了130 t该农产品．以X(单位：t,100≤X≤150)表示下一个销售季度内的市场需求量，T(单位：元)表示下一个销售季度内经销该农产品的利润．

    (1)将T表示为X的函数；
    (2)根据直方图估计利润T不少于57 000元的概率；
    (3)在直方图的需求量分组中，以各组的区间中点值代表该组的各个值，并以需求量落入该区间的频率作为需求量取该区间中点值的概率(例如：若需求量X∈[100,110)，则取X＝105，且X＝105的概率等于需求量落入[100,110)的频率)，求T的数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2013年某市某区高考文科数学成绩抽样统计如下表：
    （1）求出表中m、n、M、N的值，并根据表中所给数据在下面给出的坐标系中画出频率分布直方图；（纵坐标保留了小数点后四位小数）

    （2）若2013年北京市高考文科考生共有20000人，试估计全市文科数学成绩在90分及90分以上的人数；
    （3）香港某大学对内地进行自主招生，在参加面试的学生中，有7名学生数学成绩在140分以上，其中男生有4名，要从7名学生中录取2名学生，求其中恰有1名女生被录取的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    对甲、乙两种商品重量的误差进行抽查，测得数据如下(单位：mg)：
    甲：13　15　14　14　9　14　21　9　10　11
    乙：10　14　9　12　15　14　11　19　22　16
    (1)画出样本数据的茎叶图，并指出甲、乙两种商品重量误差的中位数；
    (2)计算甲种商品重量误差的样本方差；
    (3)现从重量误差不低于15的乙种商品中随机抽取2件，求重量误差为19的商品被抽中的概率．

    查看答案和解析>>

    同步练习册答案