
汽车是碳排放量比较大的行业之一,某地规定,从2014年开始,将对二氧化碳排放量超过 的轻型汽车进行惩罚性征税。检测单位对甲、乙两品牌轻型汽车各抽取5辆进行二氧化碳排放量检测,记录如下(单位:
的轻型汽车进行惩罚性征税。检测单位对甲、乙两品牌轻型汽车各抽取5辆进行二氧化碳排放量检测,记录如下(单位: ).
).
经测算得乙品牌轻型汽车二氧化碳排放量的平均值为 .
.
(1)从被检测的5辆甲品牌轻型汽车中任取2辆,则至少有一辆二氧化碳排放量超过 的概率是多少?
的概率是多少?
(2)求表中 的值,并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性.
的值,并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性.
(1) ;(2)乙品牌轻型汽车二氧化碳排放量的稳定性好.
;(2)乙品牌轻型汽车二氧化碳排放量的稳定性好.
解析试题分析:(1)从题目给出的表格上可知任取2辆共有10种不同结果. 设“至少有一辆二氧化碳排放量超过130g/km”为事件A,则事件A包含7种不同的结果,因此概率为 ;(2)先求出甲种品牌轻型汽车二氧化碳排放量的平均数为:
;(2)先求出甲种品牌轻型汽车二氧化碳排放量的平均数为: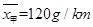 ,已知乙品牌二氧化碳排放量的平均值为
,已知乙品牌二氧化碳排放量的平均值为 ,那么还需要求出两种品牌汽车的方差分别是
,那么还需要求出两种品牌汽车的方差分别是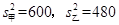 .所以乙品牌轻型汽车二氧化碳排放量的稳定性好.
.所以乙品牌轻型汽车二氧化碳排放量的稳定性好.
试题解析:(1)从被检测的5辆甲品牌的轻型汽车中任取2辆,共有10种不同的二氧化碳排放量结果:(80,110),(80,120),(80,140),(80,150),(110,120),(110,140),(110,150),(120,140),(120,150),(140,150).
设“至少有一辆二氧化碳排放量超过130g/km”为事件A,则事件A包含以下7种不同的结果:
(80,140),(80,150),(110,140),(110,150),(120,140),(120,150),(140,150)
∴ 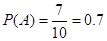 .
.
答:至少有一辆二氧化碳排放量超过130g/km的概率为 .
.
(2)由题可知,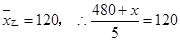 ,解得
,解得 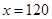 .
.
又
∴ 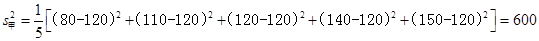 ,
,
∴ 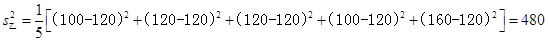 ,
,
∵ 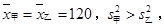
∴ 乙品牌轻型汽车二氧化碳排放量的稳定性好.
考点:古典概型概率公式;用样本数字特征估计总体.


科目:高中数学 来源: 题型:解答题
为调查乘客的候车情况,公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间(单位:分钟)作为样本分成5组,如下表所示: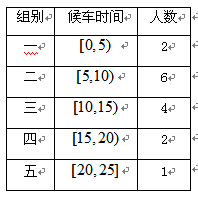
(1)估计这60名乘客中候车时间少于10分钟的人数;
(2)若从上表第三、四组的6人中随机抽取2人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某班同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
| 组 数 | 分 组 | 低碳族的人数 | 占本组的频率 |
| 第一组 | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | p |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | 0.3 |
| 第六组 | [50,55] | 15 | 0.3 |


| P(χ2≥x0) | 0.050 | 0.010 | 0.001 |
| x0 | 3.841 | 6.635 | 10.828 |
| 年龄组 是否低碳族 | 青 年 | 老 年 | 总 计 |
| 低碳族 | | | |
| 非低碳族 | | | |
| 总计 | | | |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某高校组织自主招生考试,其有2 000名学生报名参加了笔试,成绩均介于195分到275分之间,从中随机抽取50名同学的成绩进行统计,将统计结果按如下方式分成八组:第一组[195,205),第二组[205,215),……,第八组[265,275).如图是按上述分组方法得到的频率分布直方图.
(1)从这2 000名学生中,任取1人,求这个人的分数在255~265之间的概率约是多少?
(2)求这2 000名学生的平均分数;
(3)若计划按成绩取1 000名学生进入面试环节,试估计应将分数线定为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校高一年级 名学生参加数学竞赛,成绩全部在
名学生参加数学竞赛,成绩全部在 分至
分至 分之间,现将成绩分成以下
分之间,现将成绩分成以下 段:
段:
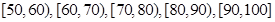 ,据此绘制了如图所示的频率分布直方图.
,据此绘制了如图所示的频率分布直方图. 
(1)求成绩在区间 的频率;
的频率;
(2)从成绩大于等于 分的学生中随机选
分的学生中随机选 名学生,其中成绩在
名学生,其中成绩在 内的学生人数为
内的学生人数为 ,求
,求 的分布列与均值.
的分布列与均值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表.
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某种报纸,进货商当天以每份1元从报社购进,以每份2元售出.若当天卖不完,剩余报纸报社以每份0.5元的价格回收.根据市场统计,得到这个季节的日销售量X(单位:份)的频率分布直方图(如图所示),将频率视为概率.
(1)求频率分布直方图中a的值;
(2)若进货量为n(单位:份),当n≥X时,求利润Y的表达式;
(3)若当天进货量n=400,求利润Y的分布列和数学期望E(Y)(统计方法中,同一组数据常用该组区间的中点值作为代表).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某班同学利用寒假进行社会实践,对年龄在 的人群随机抽取
的人群随机抽取 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:

(1)补全频率分布直方图,并求 的值;
的值;
(2)从年龄在 的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在
的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)为了解某校今年高一年级女生的身体素质状况,从该校高一年级女生中抽取了一部分学生进行“掷铅球”的项目测试,成绩低于5米为不合格,成绩在5至7米(含5米不含7米)的为及格,成绩在7米至11米(含7米和11米,假定该校高一女生掷铅球均不超过11米)为优秀.把获得的所有数据,分成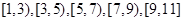 五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在9米到11米之间.
五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在9米到11米之间.
(1)求实数 的值及参加“掷铅球”项目测试的人数;
的值及参加“掷铅球”项目测试的人数;
(2)若从此次测试成绩最好和最差的两组中随机抽取2名学生再进行其它项目的测试,求所抽取的2名学生自不同组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com